2025. 4. 14. 00:31ㆍ머신러닝&딥러닝/생성모델
이 자료는 Google Research Team의 Calvin Luo가 2022년 Diffusion model의 전반적인 튜토리얼을 위해 작성한 자료이다. 원문도 꽤 이해하기 쉽진 않게 쓰여 있지만, 공부하는 차원에서 정리해 보았다.
Introduction : Generative Models
Generative model이란 무엇인가? x의 distribution p(x)를 실제와 가깝게 근사하는 모델을 말한다. (distribution p를 얻으면, 생성은 해당 분포에서 샘플링하는 것으로 할 수 있다)
GM은 세 개의 클래스가 있다. 첫째는 adversarial manner로 훈련되는 GAN 계열이다. 둘째는 likelihood-based manner 로 훈련되는 autoregressive model, normalizing flow, VAE가 있다. 셋째는 EBM이며, 이의 score를 모델링하기도 한다.
Diffusion model은 likelihood-based manner로도 해석할 수도 있고, score로도 해석할 수도 있다. 따라서 두 번째와 세 번째 클래스의 어중간한 녀석이다.
Background
GM을 이해하기 위해서는 ELBO의 개념을 이해하는 것이 필수적이다. ELBO의 식을 여러 번 유도해보자.
Introduction에서도 설명했듯이 GM의 objective는 x의 분포 p(x)의 likelihood를 최대화하는 것이다. 그러나 이는 대부분의 경우 intractable하다. 따라서, "evidence"라 불리는 log likelihood $logp(x)$의 하한선을 maximize하는 것을 proxy objective로 한다. 이를 위해, evidence의 하한선을 최대화하는 전략을 쓰고, 그 하한선을 ELBO라고 한다.
ELBO는 아래와 같이 Jensen's inequality를 쓰면, 학습가능한 variational distribution q를 이용해 나타낼 수 있다.

그런데, Jensen's inequality를 쓰면 등호성립이 언제 되는지, 즉 optimization이 일어날 때 무슨 과정이 일어나는지 한눈에 보기 어렵다. 따라서 Bayes rule로 두 번째 방법의 유도를 할 수 있다.

두 번재 유도를 보면, ELBO의 등호성립조건은 variational distribution q(z|x)와 p(z|x)의 KL이 0일 때임을 알 수 있어 더 직관적이다.
그런데 KL term도 아직 덜 직관적이다. q(z|x)는 우리가 optimization해야 하는, 원본데이터 x에서 latent 가 어떻게 만들어지는지에 대한 variational posterior인데, p(z|x)는 무엇인가? 이는 intractable한 값이다. 따라서, ELBO+KL = 상수(evidence)인 상황에서, KL을 최소화하는 것이 아니라 ELBO를 최대화하는 전략을 취하는 것이다.
Variational Autoencoders
VAE에서 ELBO maximization이 어떻게 이루어지는지 보자. VAE에서 variational posterior는 학습가능한 encoder로 볼 수 있다.

Hierarchical Variational Autoencoders
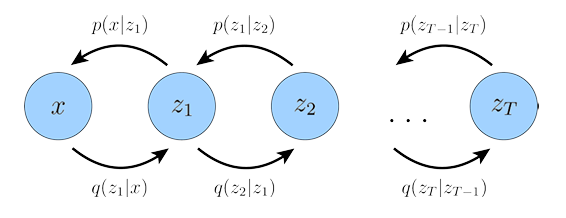
HVAE는 VAE의 latent z를 T개 쌓아서 계층화한 구조이다. 이때 joint distribution은 x, z1, ..., zT에 대해 나타내어지며, ELBO 식은 아래와 같이 전개할 수 있다.
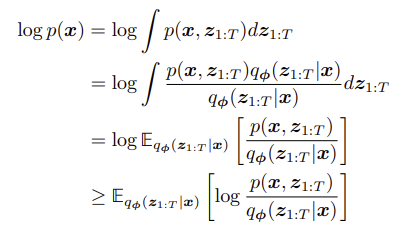
HVAE에 Markov assumption (각 latent는 직전 latent에만 영향받는다)를 추가하면 MHVAE(Markovian HVAE)가 되는데, Markov chain 특징에 따라 ELBO를 아래와 같이 한 번 더 전개할 수도 있다.

Variational Diffusion Models
VDM은 MHVAE 세팅에서 세 가지 조건을 추가한 것으로 볼 수 있다.
- latent의 차원은 원본의 차원과 같다. (z 대신 xi 노테이션을 쓸 수 있음)
- latent encoder는 학습되지 않는다.
- latent encoder는 이전 단계 latent에 대한 gaussian distribution으로 모델링되며, 마지막 단계 x_T는 standard gaussian이다.
첫 번째 조건에 의하면, variational posterior는 아래와 같이 식을 쓸 수 있다.
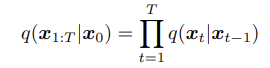
또한, 두 번째와 세 번째 조건에 따라, gaussian parameter를 이용한 모델링으로 forward kernel을 아래와 같이 정의할 수 있다.

이때 $\alpha_t$는 학습이 될 수도 있고 고정될 수도 있다. 중요한 것은 hierarchical depth t에 따라 고유한 값을 갖는다는 점이다.
마지막으로, 세 번째 조건에 따라, joint distribution은 아래와 같이 쓸 수 있으며, $p(x_T)$는 gaussian이다.

이것을 이용해서 ELBO 식을 전개하고 optimize해야 할 식을 만들어 보자.

Jensen Inequality로 ELBO를 만들고, Markovian 특징을 이용해 저개하는 것까지는 똑같으나, 분자에서의 $p_\theta (x_0 | x_1) $ (이 부분은 VAE에서의 reconstruction loss와 유사한 term이 될 부분), 분모에서의 $q(x_T|x_{T-1})$ (이 부분은 VAE의 prior matching과 유사한 term이 될 부분) 을 따로 빼어 정리한다.
최종적으로, VDM의 loss term은 아래와 같이 세 가지 부분으로 나누어진다.
- Reconstruction loss term
- Prior matching term
- Consistency term
Reconstruction loss term은 VAE와 유사하게 구성되며, 첫 번째 latent로 x_0를 복원하는 작업을 의미한다. Prior matching term은 최종 forward kernel 적용 후 gaussian prior에 도달해야 함을 의미한다. 마지막으로, consistency term은 VAE에는 없던 term인데, 이는 각 중간 스텝의 reverse kernel이 forward kernel과 consistent해야 함을 의미한다.
이 세 가지 term 중 가장 time-consuming한 것은 세 번째, consistency term이다. 이 term은 $x_t$를 추정하기 위해 $x_t-1$과 $x_t+1$의 두 가지 term을 모두 사용해야 하는데, 이는 Monte Carlo estimation의 variance를 너무 키울 수 있다.
여기서 등장하는 중요한 아이디어는, $q(x_t | x_t-1)$을 계산할 때 markovian property에 의해 계산에 영향을 주지 않는 $x_0$을 하나 더 붙여서 $q(x_t | x_t-1, x_0)$으로 계산하자는 것이다. 그러면 consistency term을 아래와 같이 다시 쓸 수 있다.

그러면 일부 항이 telescoping되면서 아래와 같이 다시 정리된다.
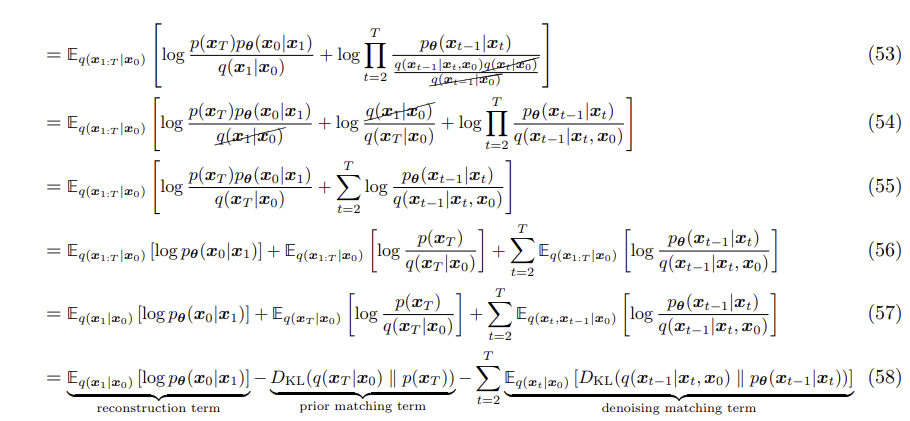
마지막 58번 식에서의 objective만 보면, 크게 두 가지가 달라졌음을 확인할 수 있다.
- Prior matching term에서 $x_T-1$이 아닌 $x_0$으로 conditioning 되어있다.
- Consistency term 대신 denoising matching term이 생겼다.
Prior matching term은 우리의 가정에 의하면 0으로 날려버릴 수 있다. (parameter가 없어 optimization할 수도 없다) 따라서, Recon term과 denoising matching term만 고려하면 된다.
Denoising matching term은 학습되지 않는 term인 $q(x_{t-1} | x_t, x_0)$ 을 gt로 하여 $p_\theta(x_{t-1}|x_t)$ 를 학습시키는 구조이다. $q(x_{t-1} | x_t, x_0)$는 bayes rule을 이용하여 아래와 같이 정리할 수 있다.

이때 $q(x_{t} | x_{t-1}, x_0) = q(x_t | x_{t-1}$이다. 또한, 나머지 두 개의 forward kernel을 계산하기 위해, $q(x_t|x_0)$을 아래와 같이 전개할 수 있다.
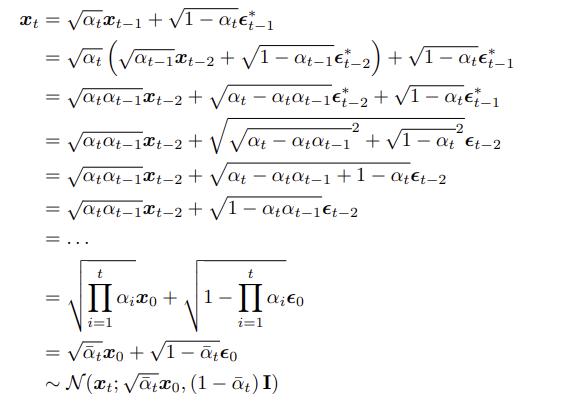
이 식을 bayes rule로 정리했던 부분에 대입하면(계산 생략) $q(x_{t-1} | x_t, x_0)$를 아래와 같이 계산 가능한 분포로 나타낼 수 있다.

이 식을 보면, $q(x_{t-1} | x_t, x_0)$는 정규분포로 나타낼 수 있으며, 평균 $\mu$는 $x_t, x_0$의 식이고, variance는 알파 상수의 조합임을 알 수 있다.
이제, $p_\theta (x_{t-1} | x_t)$ 가 위 분포로 근사되도록 하려면, $p_\theta (x_{t-1} | x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \sigma_t^2 \mathbf{I})$ 로 나타낼 수 있고, variance는 q에서 상수이므로 p에서 학습될 필요가 없다. 따라서, $x_t, t$에 의존하는 $\mu_\theta$만 모델링하면 된다.
특히, 두 gaussian 간의 KL divergence 공식을 이용하여 정리해 보면, $q(x_{t-1} | x_t, x_0)$와 $p_\theta (x_{t-1} | x_t)$는두 분포의 평균의 square error에 상수가 곱해진 형태로 정리할 수 있다.
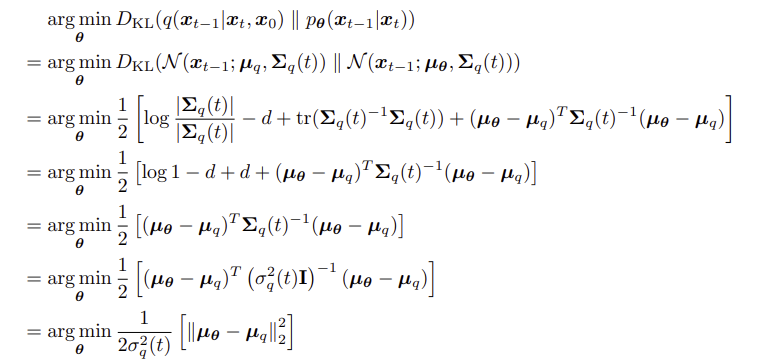
위에서 $q(x_{t-1} | x_t, x_0)$는 아래와 같음을 보였고,

$\mu_\theta$는 $x_t, t$에 의해 정해지므로 아래와 같이 모델링할 수 있다.

이 두 식의 square error를 비교하면, 결국 마지막 항만 차이가 나기 때문에 $x_\theta$와 $x_0$간의 square error로 식이 바뀐다.
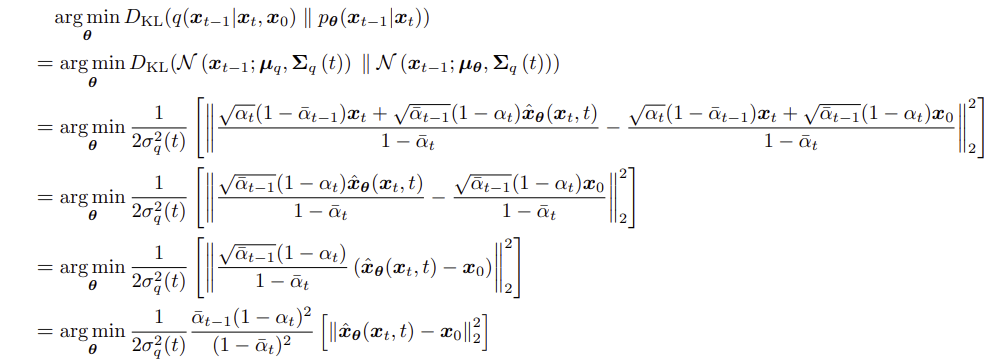
결국 시간과 $x_t$에 의해 예측된 $x_0$와 원본의 차이를 줄이는 것을 objective로 하면 된다.
Learning DM parameters
위의 식에서 $\alpha_t$를 학습되지 않는 t에 따른 상수열로 고정한다면, $x_\theta$와 $x_0$의 L2 loss term 앞의 항은 optimize할 게 없으므로 그냥 날려도 된다. 하지만, 이러한 alphas가 학습된다면 어떻게 될까? 만약 모든 t에 대한 alpha에 parameter를 부여하여 학습되도록 한다면, 계산이 너무 복잡해질 것이므로 Kingma et al.은 Variational Diffusion Models 논문에서 SNR value를 이용하였다. 위에서 $\sigma_q$를 대입하여 알파에 대한 식으로 정리하면, objective function은 아래와 같이 변한다.
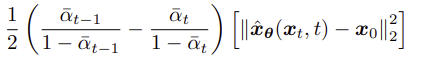
이때 $q(x_t | x_0)$은 아래에서 샘플링된다.

즉, SNR의 정의인 $\sigma^2 / \mu^2$에 따르면, 아래와 같이 이해할 수 있다.

이는 objective function에 대입하면 아래와 같이 변한다.

그러면 SNR을 analytic하게 정리할 수 있는 감소함수로 parametrize할 수 있게 되고, 아래와 같이 모델링할 수 있다.
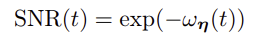
Three Equivalent Interpretations
위 내용은 VDM을 noising한 $x_t$에서 $x_0$을 예측하는 것(-> 원본이미지 예측)으로 해석하여 푼 결과인데, 이것 말고도 두 가지 해석이 더 존재한다.
해석 2 : 노이즈 예측
$x_t$는 아래와 같이 쓸 수 있다.

이 식을 $x_0$에 대해 정리하면 아래와 같다.

이를 아래 $\mu_q$식에 대입할 수 있다.

그러면 $x_0$이 $\epsilon_0$에 대한 식으로 바뀌고, opmizing해야 하는 denoising matching term을 아래와 같이 새로 정리할 수 있다.
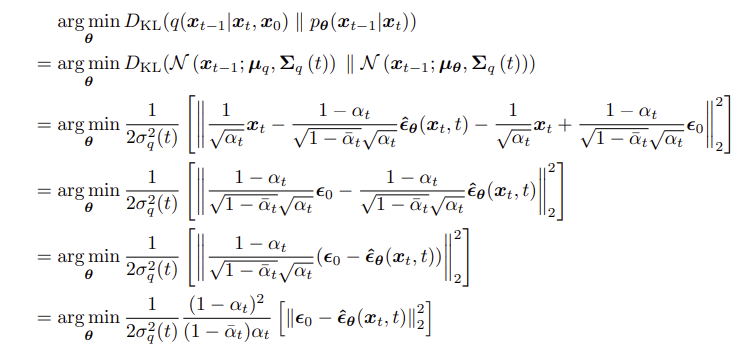
위에서 $x_\theta (x_t, t)$를 $x_0$에 대해 optimize했던 것과 달리, 이제는 noise 자체를 예측해 optimize할 수 있게 된 것이다. 이렇게 노이즈 예측을 하는 방식으로 optimizing하는 것이 원본 이미지 예측을 하는 방식으로 optimizing하는 것보다 성능이 좋다느 것은 DDPM(2020) 논문 등을 통해 밝혀졌다.
해석 3 : Score 해석
이 해석은 noizy observation $z$에 대해 posterior mean $\mu_z$를 추정하기 위해 Tweedie's formula를 적용하는 것으로부터 시작된다.

이제, diffusion forward kernel 과 Tweedie's formula를 아래와 같이 연립하자.
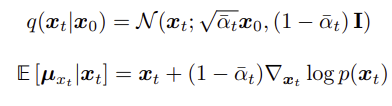
그러면 아래 식을 얻는다.
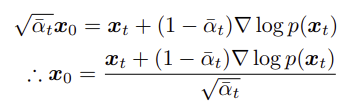
이러한 결과를 1번 해석에서 얻었던 $\mu_q$식에 대입하면, 아래와 같이 나타낼 수 있다.

이 식을 이용하여 해석 1, 2와 유사한 아이디어로, $p_\theta (x_{t-1} | x_t )$ 을 $x_t, t$에 의해 예측되는 score 값 $s_\theta$과 $x_t$의 식으로 나타낼 수 있고, 아래와 같이 KL divergence를 계산할 수 있다.
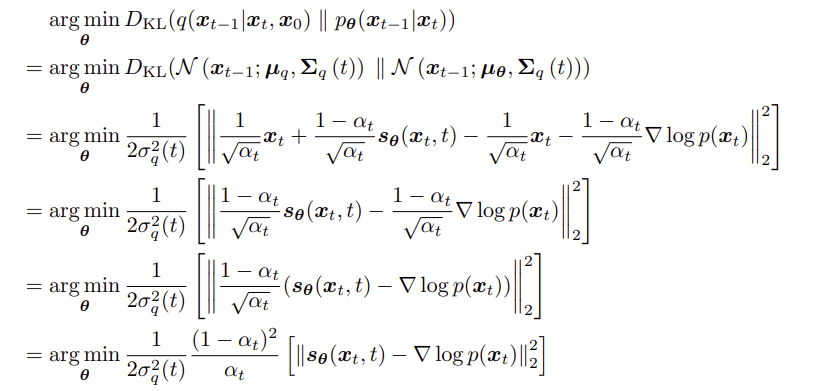
'머신러닝&딥러닝 > 생성모델' 카테고리의 다른 글
| cGAN (2014)의 간단한 오버뷰 (2) | 2025.01.22 |
|---|---|
| OpenAI Guided-diffusion 코드분석 Part 1: Gaussian Diffusion 유틸 (0) | 2024.08.18 |
| VAE latent는 어떻게 생겼을까? (feat. PCA) (0) | 2024.08.14 |
| Classifier Guidance 논문리뷰 (Diffusion Models Beat GANs on Image Synthesis, 2021) (0) | 2024.08.14 |
| DDIM 논문 리뷰 - 샘플링 가속과 consistency (1) | 2024.08.14 |