2024. 8. 18. 20:53ㆍ머신러닝&딥러닝/생성모델
OpenAI에서 제공하는 Guided-diffusion repository(https://github.com/openai/guided-diffusion)는 Ho et al.의 DDPM 모델부터 DDIM 샘플링, 그리고 classifier guidance까지 줄 수 있는 다양한 디퓨전 유틸리티가 들어 있다.
GitHub - openai/guided-diffusion
Contribute to openai/guided-diffusion development by creating an account on GitHub.
github.com
Classifier guidance는 지난 포스팅 (https://cascade.tistory.com/120)에서 설명했으니 본 포스팅에서는 OpenAI guided-diffusion 코드를 설명하는 것으로 바로 진행하고자 한다.
Classifier Guidance 논문리뷰 (Diffusion Models Beat GANs on Image Synthesis, 2021)
본 논문은 OpenAI에서 발표한, unconditional image generation만 가능했던 디퓨전 계열 아키텍처에 최초로 컨디셔닝을 적용한 논문이다. 이를 Classifier Guidance라고 한다. IntroductionDDPM이 등장하였지만, 아직
cascade.tistory.com
전체 구조
코드 유틸리티가 대부분 저장되어 있는 guided-diffusion 폴더에는 아래와 같은 파일들이 들어 있다. 각각의 기능을 살펴 보자.
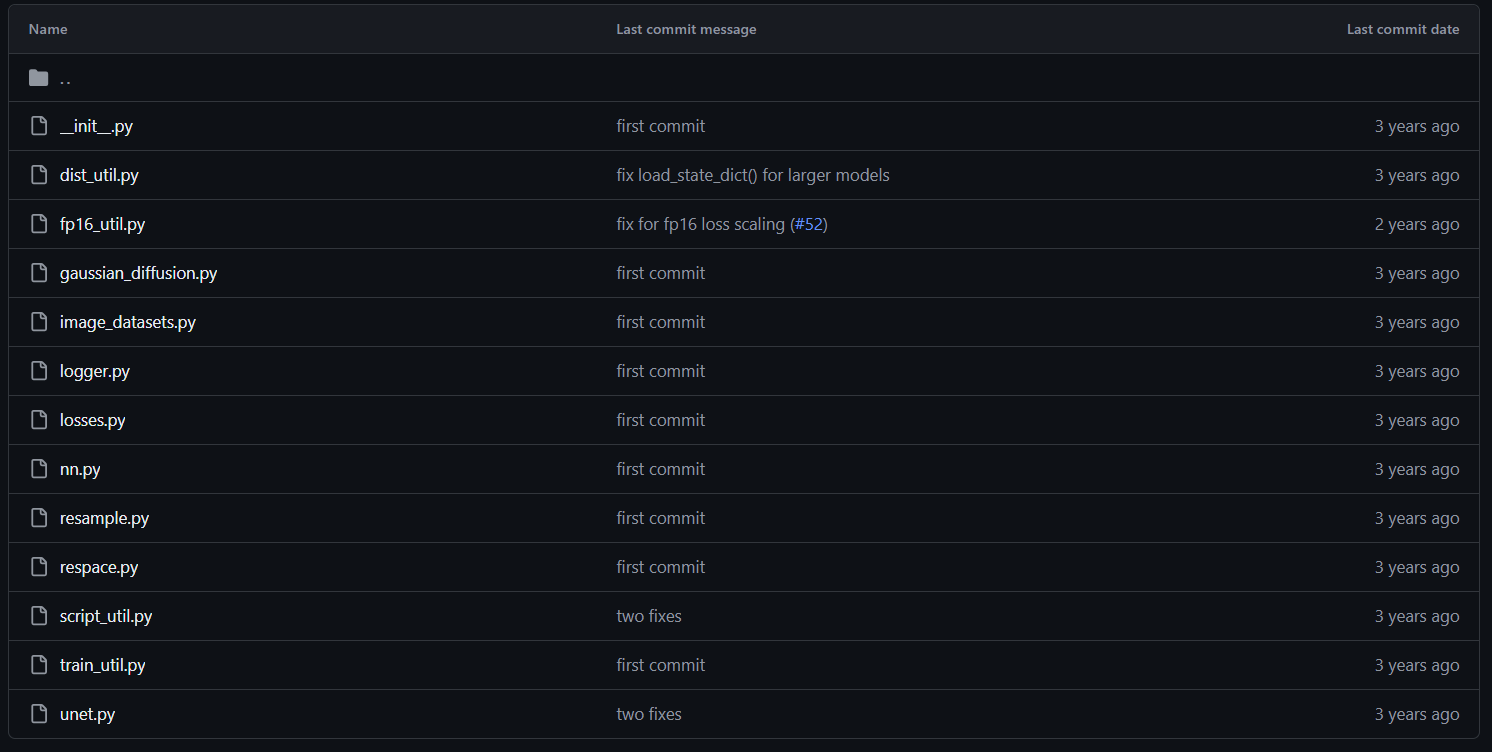
| dist_util | distributed training 지원 |
| fp16_util | half precision 관련 유틸 |
| gaussian_diffusion | 디퓨전 관련 유틸리티가 포함된 핵심 코드 |
| image_datasets | Custom dataset의 정의, load_data 함수 등 데이터 코드 |
| logger | 콘솔에 로깅하는 유틸 |
한때 병원 내부망 환경에다가 guided-diffusion 환경설정을 하려다가, dist_util의 주요 requirement인 mpi4py(GPU parallel 라이브러리)가 충돌이 나서 애먹었던 적이 있다. (병원 내부망에서는 보안상 GPU parallel이 안 된다.)
| losses | kld, log likelihood 등 디퓨전에서 쓸 loss들 |
| nn | Neural Network 관련 각종 유틸 |
| resample | 디퓨전 학습에서 timestep sampling 조절에 관한 코드 |
| respace | DDIM sampling trajectory 등 샘플링 스텝을 조절하는 코드 |
| script_util | argparser로 들어온 인자를 반영하여 모델 등 생성하는 코 |
| train_util | train_loop에 관한 코드 |
| unet | ADM-G/U에 해당하는 denoising U-Net 코드 |
Util 분석 : guided_diffusion/gaussian_diffusion.py
베타 스케줄러
- Ho et al. 의 DDPM에서 beta들은 등간격으로 scheduling되므로 torch.linspace를 이용하여 등간격으로 샘플링한다. 이때 timestep의 수가 커지면 scale이 작아져 beta값이 반비례하게 작아진다.
- Nichol&Dhariwal의 IDDPM에서 beta들은 cosine scheduling된다. 즉 아래 식(s=0.008)을 따라 샘플링하면 되는데 이는 알파에 대한 식이므로 beta_for_alpha_bar 함수를 따로 정의해서 가져온다.
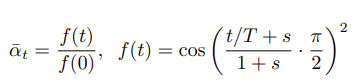
def get_named_beta_schedule(schedule_name, num_diffusion_timesteps):
"""
Get a pre-defined beta schedule for the given name.
The beta schedule library consists of beta schedules which remain similar
in the limit of num_diffusion_timesteps.
Beta schedules may be added, but should not be removed or changed once
they are committed to maintain backwards compatibility.
"""
if schedule_name == "linear":
# Linear schedule from Ho et al, extended to work for any number of
# diffusion steps.
scale = 1000 / num_diffusion_timesteps
beta_start = scale * 0.0001
beta_end = scale * 0.02
return np.linspace(
beta_start, beta_end, num_diffusion_timesteps, dtype=np.float64
)
elif schedule_name == "cosine":
return betas_for_alpha_bar(
num_diffusion_timesteps,
lambda t: math.cos((t + 0.008) / 1.008 * math.pi / 2) ** 2,
)
else:
raise NotImplementedError(f"unknown beta schedule: {schedule_name}")
아래 식이 성립하므로, 코드와 같이 alpha_bar라는 람다함수에서 beta를 계산해서 betas 리스트에 추가할 수 있다.
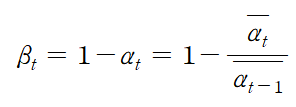
위 코드에서 정의한 람다함수를 잘 보면, alpha_bar에 들어가는 t는 정수 timestep이 아니라 timestep을 num_diffusion_timesteps으로 나눈 값(즉, t/T) 으로 0과 1 사이이다.
def betas_for_alpha_bar(num_diffusion_timesteps, alpha_bar, max_beta=0.999):
"""
Create a beta schedule that discretizes the given alpha_t_bar function,
which defines the cumulative product of (1-beta) over time from t = [0,1].
:param num_diffusion_timesteps: the number of betas to produce.
:param alpha_bar: a lambda that takes an argument t from 0 to 1 and
produces the cumulative product of (1-beta) up to that
part of the diffusion process.
:param max_beta: the maximum beta to use; use values lower than 1 to
prevent singularities.
"""
betas = []
for i in range(num_diffusion_timesteps):
t1 = i / num_diffusion_timesteps
t2 = (i + 1) / num_diffusion_timesteps
betas.append(min(1 - alpha_bar(t2) / alpha_bar(t1), max_beta))
return np.array(betas)
ModelMeanType은 model이 어떤 값을 예측할지를 결정한다. enum은 python에서 enumerate할 수 있는 객체를 만드는데, enum.auto()를 이용하면 PREVIOUS_X에 1, START_X에 2, EPSILON에 3의 인덱스가 부여된다.
class ModelMeanType(enum.Enum):
"""
Which type of output the model predicts.
"""
PREVIOUS_X = enum.auto() # the model predicts x_{t-1}
START_X = enum.auto() # the model predicts x_0
EPSILON = enum.auto() # the model predicts epsilon
ModelVarType은 모델의 output variance를 어떤 것으로 사용할지 나타낸다. Learned variance는 DDPM이 "이론적으로" 적용되었을 때를 말하며, 아래 식의 sigma theta이다.
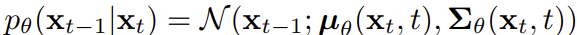
DDPM 논문의 저자 Ho et al. 도 학습 안전성과 효율성을 위해 sigma를 고정한 채로 사용하였다. 분산을 크게 고정하면 diversity가 올라가고, 작게 고정하면 fidelity가 올라간다. 또한, Nichol&Dhariwal의 IDDPM에서는 분산을 고정시키는 게 아니라 최대분산과 최소분산 사이에서 학습되도록 했다. 즉 아래 식에서 interpolation 정도를 조절해주는 v를 결정하는 것이다.
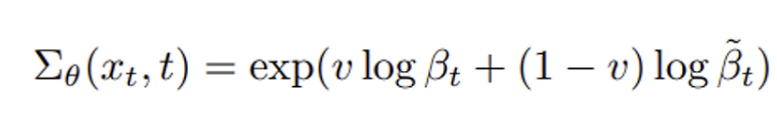
class ModelVarType(enum.Enum):
"""
What is used as the model's output variance.
The LEARNED_RANGE option has been added to allow the model to predict
values between FIXED_SMALL and FIXED_LARGE, making its job easier.
"""
LEARNED = enum.auto()
FIXED_SMALL = enum.auto()
FIXED_LARGE = enum.auto()
LEARNED_RANGE = enum.auto()
Diffusion의 loss는 크게 두 가지, MSE loss와 KL divergence loss를 사용한다. MSE loss는 predicted noise(epsilon_theta)와 실제 noise (epsilon) 간의 차이를 볼 때 사용된다. 분산이 고정되어 있다면 MSE loss만 사용해도 되지만, 분산도 학습되는 경우 KL loss까지 함께 사용된다. Rescaling은 학습의 안정성을 위해 상수배를 곱하는 것을 말한다. VLB를 사용하는 경우 kl loss를 써야 하므로, is_vb라는 메소드를 따로 넣어 주었다.
class LossType(enum.Enum):
MSE = enum.auto() # use raw MSE loss (and KL when learning variances)
RESCALED_MSE = (
enum.auto()
) # use raw MSE loss (with RESCALED_KL when learning variances)
KL = enum.auto() # use the variational lower-bound
RESCALED_KL = enum.auto() # like KL, but rescale to estimate the full VLB
def is_vb(self):
return self == LossType.KL or self == LossType.RESCALED_KL
Gaussian Diffusion
- betas는 베타값들을 담고 있는 1D numpy array이다. T, T-1, ..., 1까지 역순으로 담긴다.
- model_mean_type은 class ModelMeanType에서 설정했던, 모델이 예측할 값을 받는다.
- model_var_type은 class ModelVarType에서 설정했던, output variance의 종류를 받는다.
- loss_type은 class LossType에서 설정했던, loss type의 종류(rescaled + MSE/KL)을 받는다.
- rescale_timesteps를 boolean 변수로, True로 설정되면 본 논문처럼 timestep이 0, 1, ..., 1000으로 고정된다.
이 __init__에서 betas를 이용하여 미리 저장해 놓는 상수는 아래와 같다.
- 기본 상수
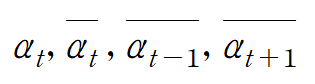
- DDPM forward에 필요한 상수 : q(x_t | x_t-1)
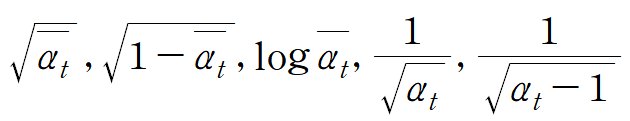
- posterior 관련 상수 : q(x_t-1 | x_t, x_0)
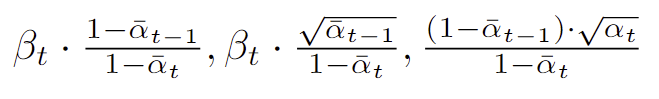
이 중 첫 번째 식 (posterior_variance) 에 log를 씌워 posterior_log_variance를 만드는데, posterior_variance의 첫 항은 0이므로 두 번째 항을 첫 번째 항으로 가져온 뒤 log를 씌운다.
def __init__(
self,
*,
betas,
model_mean_type,
model_var_type,
loss_type,
rescale_timesteps=False,
):
self.model_mean_type = model_mean_type
self.model_var_type = model_var_type
self.loss_type = loss_type
self.rescale_timesteps = rescale_timesteps
# Use float64 for accuracy.
betas = np.array(betas, dtype=np.float64)
self.betas = betas
assert len(betas.shape) == 1, "betas must be 1-D"
assert (betas > 0).all() and (betas <= 1).all()
self.num_timesteps = int(betas.shape[0])
alphas = 1.0 - betas
self.alphas_cumprod = np.cumprod(alphas, axis=0)
self.alphas_cumprod_prev = np.append(1.0, self.alphas_cumprod[:-1])
self.alphas_cumprod_next = np.append(self.alphas_cumprod[1:], 0.0)
assert self.alphas_cumprod_prev.shape == (self.num_timesteps,)
# calculations for diffusion q(x_t | x_{t-1}) and others
self.sqrt_alphas_cumprod = np.sqrt(self.alphas_cumprod)
self.sqrt_one_minus_alphas_cumprod = np.sqrt(1.0 - self.alphas_cumprod)
self.log_one_minus_alphas_cumprod = np.log(1.0 - self.alphas_cumprod)
self.sqrt_recip_alphas_cumprod = np.sqrt(1.0 / self.alphas_cumprod)
self.sqrt_recipm1_alphas_cumprod = np.sqrt(1.0 / self.alphas_cumprod - 1)
# calculations for posterior q(x_{t-1} | x_t, x_0)
self.posterior_variance = (
betas * (1.0 - self.alphas_cumprod_prev) / (1.0 - self.alphas_cumprod)
)
# log calculation clipped because the posterior variance is 0 at the
# beginning of the diffusion chain.
self.posterior_log_variance_clipped = np.log(
np.append(self.posterior_variance[1], self.posterior_variance[1:])
)
self.posterior_mean_coef1 = (
betas * np.sqrt(self.alphas_cumprod_prev) / (1.0 - self.alphas_cumprod)
)
self.posterior_mean_coef2 = (
(1.0 - self.alphas_cumprod_prev)
* np.sqrt(alphas)
/ (1.0 - self.alphas_cumprod)
)
q(x_t | x_0)의 분포를 리턴하는 함수로, mean과 variance를 미리 정의해 놓은 식을 이용하여 계산한다.
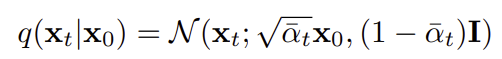
def q_mean_variance(self, x_start, t):
"""
Get the distribution q(x_t | x_0).
:param x_start: the [N x C x ...] tensor of noiseless inputs.
:param t: the number of diffusion steps (minus 1). Here, 0 means one step.
:return: A tuple (mean, variance, log_variance), all of x_start's shape.
"""
mean = (
_extract_into_tensor(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start
)
variance = _extract_into_tensor(1.0 - self.alphas_cumprod, t, x_start.shape)
log_variance = _extract_into_tensor(
self.log_one_minus_alphas_cumprod, t, x_start.shape
)
return mean, variance, log_variance
이때 _extract_into_tensor 메소드가 이용되는데, 이는 상수들이 저장된 1D numpy array에서 해당 timestep에 해당하는 상수들을 배치 사이즈만큼 뽑아서 가져온다.
def _extract_into_tensor(arr, timesteps, broadcast_shape):
"""
Extract values from a 1-D numpy array for a batch of indices.
:param arr: the 1-D numpy array.
:param timesteps: a tensor of indices into the array to extract.
:param broadcast_shape: a larger shape of K dimensions with the batch
dimension equal to the length of timesteps.
:return: a tensor of shape [batch_size, 1, ...] where the shape has K dims.
"""
res = th.from_numpy(arr).to(device=timesteps.device)[timesteps].float()
while len(res.shape) < len(broadcast_shape):
res = res[..., None]
return res.expand(broadcast_shape)
q_sample 메소드는 위에서 정의한 q_mean_variance로부터 만든 분포 q(x_t | x_0) 로부터 샘플링하는 코드이다. 즉, x_start에 t timestep만큼 노이징하여 x_t를 리턴하는 코드이다. (근데 사실, alphas 로부터 q의 mean, variance가 도출되고, alphas로부터 x_t가 직접 도출되므로 x_t를 얻는 데 mean과 variance가 직접적으로 필요하진 않다.)
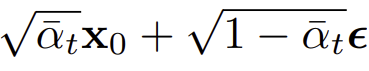
def q_sample(self, x_start, t, noise=None):
"""
Diffuse the data for a given number of diffusion steps.
In other words, sample from q(x_t | x_0).
:param x_start: the initial data batch.
:param t: the number of diffusion steps (minus 1). Here, 0 means one step.
:param noise: if specified, the split-out normal noise.
:return: A noisy version of x_start.
"""
if noise is None:
noise = th.randn_like(x_start)
assert noise.shape == x_start.shape
return (
_extract_into_tensor(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start
+ _extract_into_tensor(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape)
* noise
)
q_posterior_mean_variance는 아래와 같은 Diffusion posterior 식을 이용한다. Diffusion posterior는 x_0과 x_t를 모두 알고 있을 때 x_t-1의 분포로, prior q(x_t | x_0)로부터 유도된다.
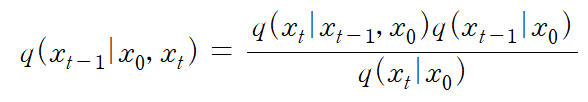
Diffusion posterior는 mu_tilde를 평균으로, beta_tilde를 분산으로 하는 아래와 같은 정규분포이다.
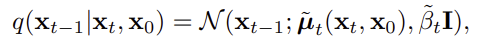
이 값들도 alphas와 betas를 이용하여, 아래와 같이 계산할 수 있다.
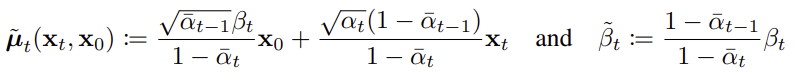
def q_posterior_mean_variance(self, x_start, x_t, t):
"""
Compute the mean and variance of the diffusion posterior:
q(x_{t-1} | x_t, x_0)
"""
assert x_start.shape == x_t.shape
posterior_mean = (
_extract_into_tensor(self.posterior_mean_coef1, t, x_t.shape) * x_start
+ _extract_into_tensor(self.posterior_mean_coef2, t, x_t.shape) * x_t
)
posterior_variance = _extract_into_tensor(self.posterior_variance, t, x_t.shape)
posterior_log_variance_clipped = _extract_into_tensor(
self.posterior_log_variance_clipped, t, x_t.shape
)
assert (
posterior_mean.shape[0]
== posterior_variance.shape[0]
== posterior_log_variance_clipped.shape[0]
== x_start.shape[0]
)
return posterior_mean, posterior_variance, posterior_log_variance_clipped
p_mean_variance는 reverse process의 분포의 평균과 분포를 이용하여 x_0를 예측하는 코드이다.
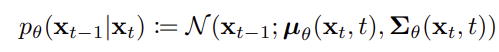
이때, 위에서 설명하였듯이 디퓨전에서 variance (sigma_theta)를 학습시킬 수도 있고, 고정된 값으로 둘 수도 있다. 또한, model이 예측하는 값이 previous, start, noise 중 무엇이 될지도 정할 수 있다.
먼저, model 파라미터에는 노이즈 예측하는 모델, 즉 학습 가능한 파라미터를 가진 denoising module이 들어간다. denoising unet은 (x, t)를 인풋으로 받아 (B, C*2, H, W) 크기의 텐서를 output으로 리턴하는데, 이는 모델의 output과 모델의 variance가 concat되어 있는 형태이므로 torch.split을 이용해 두 개로 분리해 주었다. 이때 model 의 variance가 LEARNED 모드라면 이 값을 그대로 사용하고, LEARNED_RANGE 모드(IDDPM)라면 미리 저장해둔 posterior_log_variance_clipped에서 min 분산 (beta tilde)을, betas에서 max 분산을 가져온다. 그리고 모델에서 나온 분산을 이용(frac)하여 v값을 구해 아래 식처럼 분산을 계산한다.
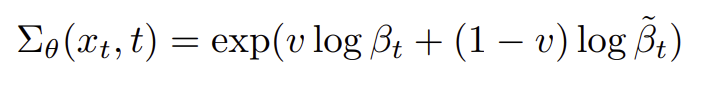
또한 분산이 학습되지 않는 FIXED 모드라면 미리 저장된 FIXED_LARGE 혹은 FIXED_SMALL 에서 분산을 가져와서 쓴다.
def p_mean_variance(
self, model, x, t, clip_denoised=True, denoised_fn=None, model_kwargs=None
):
"""
Apply the model to get p(x_{t-1} | x_t), as well as a prediction of
the initial x, x_0.
:param model: the model, which takes a signal and a batch of timesteps
as input.
:param x: the [N x C x ...] tensor at time t.
:param t: a 1-D Tensor of timesteps.
:param clip_denoised: if True, clip the denoised signal into [-1, 1].
:param denoised_fn: if not None, a function which applies to the
x_start prediction before it is used to sample. Applies before
clip_denoised.
:param model_kwargs: if not None, a dict of extra keyword arguments to
pass to the model. This can be used for conditioning.
:return: a dict with the following keys:
- 'mean': the model mean output.
- 'variance': the model variance output.
- 'log_variance': the log of 'variance'.
- 'pred_xstart': the prediction for x_0.
"""
if model_kwargs is None:
model_kwargs = {}
B, C = x.shape[:2]
assert t.shape == (B,)
model_output = model(x, self._scale_timesteps(t), **model_kwargs)
if self.model_var_type in [ModelVarType.LEARNED, ModelVarType.LEARNED_RANGE]:
assert model_output.shape == (B, C * 2, *x.shape[2:])
model_output, model_var_values = th.split(model_output, C, dim=1)
if self.model_var_type == ModelVarType.LEARNED:
model_log_variance = model_var_values
model_variance = th.exp(model_log_variance)
else:
min_log = _extract_into_tensor(
self.posterior_log_variance_clipped, t, x.shape
)
max_log = _extract_into_tensor(np.log(self.betas), t, x.shape)
# The model_var_values is [-1, 1] for [min_var, max_var].
frac = (model_var_values + 1) / 2
model_log_variance = frac * max_log + (1 - frac) * min_log
model_variance = th.exp(model_log_variance)
else:
model_variance, model_log_variance = {
# for fixedlarge, we set the initial (log-)variance like so
# to get a better decoder log likelihood.
ModelVarType.FIXED_LARGE: (
np.append(self.posterior_variance[1], self.betas[1:]),
np.log(np.append(self.posterior_variance[1], self.betas[1:])),
),
ModelVarType.FIXED_SMALL: (
self.posterior_variance,
self.posterior_log_variance_clipped,
),
}[self.model_var_type]
model_variance = _extract_into_tensor(model_variance, t, x.shape)
model_log_variance = _extract_into_tensor(model_log_variance, t, x.shape)
def process_xstart(x):
if denoised_fn is not None:
x = denoised_fn(x)
if clip_denoised:
return x.clamp(-1, 1)
return x
if self.model_mean_type == ModelMeanType.PREVIOUS_X:
pred_xstart = process_xstart(
self._predict_xstart_from_xprev(x_t=x, t=t, xprev=model_output)
)
model_mean = model_output
elif self.model_mean_type in [ModelMeanType.START_X, ModelMeanType.EPSILON]:
if self.model_mean_type == ModelMeanType.START_X:
pred_xstart = process_xstart(model_output)
else:
pred_xstart = process_xstart(
self._predict_xstart_from_eps(x_t=x, t=t, eps=model_output)
)
model_mean, _, _ = self.q_posterior_mean_variance(
x_start=pred_xstart, x_t=x, t=t
)
else:
raise NotImplementedError(self.model_mean_type)
assert (
model_mean.shape == model_log_variance.shape == pred_xstart.shape == x.shape
)
return {
"mean": model_mean,
"variance": model_variance,
"log_variance": model_log_variance,
"pred_xstart": pred_xstart,
}
다음으로, model_output을 PREVIOUS_X, START_X, EPSILON 중 원하는 형태로 바꾸어야 한다. 위 코드에서는 x_0, epsilon, x_t-1 사이에서 변환을 자유자재로 할 수 있도록 상호 변환하는 세 가지 메소드를 아래와 같이 작성해 놓았다. 세 가지 예측 형태가 왜 아래와 같이 상호변환되어 있는지는 논문의 수식을 보고 생각해 볼 것.
def _predict_xstart_from_eps(self, x_t, t, eps):
assert x_t.shape == eps.shape
return (
_extract_into_tensor(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t
- _extract_into_tensor(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape) * eps
)
def _predict_xstart_from_xprev(self, x_t, t, xprev):
assert x_t.shape == xprev.shape
return ( # (xprev - coef2*x_t) / coef1
_extract_into_tensor(1.0 / self.posterior_mean_coef1, t, x_t.shape) * xprev
- _extract_into_tensor(
self.posterior_mean_coef2 / self.posterior_mean_coef1, t, x_t.shape
)
* x_t
)
def _predict_eps_from_xstart(self, x_t, t, pred_xstart):
return (
_extract_into_tensor(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t
- pred_xstart
) / _extract_into_tensor(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape)
Classifier Guiance를 주기 위해서는 classifier gradient를 이용하여 p_mean_var를 변형해야 한다. ADM-G 모델에서는 아래와 같은 알고리즘으로 conitioning을 주었는데, 이를 아래 코드에 그대로 적용하였다.

p_mean_variance 함수를 이용하여 model로부터 계산한 p_mean과 p_var를 위와 같이 조합하는데, x_t-1은 p_mean에 scaling 상수, p_var, classifier gradient가 곱해진 새로운 평균(new_mean)으로부터 샘플링된다.
def condition_mean(self, cond_fn, p_mean_var, x, t, model_kwargs=None):
"""
Compute the mean for the previous step, given a function cond_fn that
computes the gradient of a conditional log probability with respect to
x. In particular, cond_fn computes grad(log(p(y|x))), and we want to
condition on y.
This uses the conditioning strategy from Sohl-Dickstein et al. (2015).
"""
gradient = cond_fn(x, self._scale_timesteps(t), **model_kwargs)
new_mean = (
p_mean_var["mean"].float() + p_mean_var["variance"] * gradient.float()
)
return new_mean
condition_score는 예측된 epsilon에서 classifier gradient를 반영하여 새로운 epsilon을 계산한다.
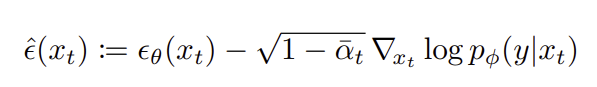
이때 p_mean_var라는 딕셔너리 형태의 인자를 받는데, 여기에 예측된 x_0와 mean을 저장한다. q_posterior_mean_variance는 posterior_mean, posterior_variance, posterior_log_variance_clipped의 세 가지를 반환하는데 이 중 posterior mean만 사용하였다.
def condition_score(self, cond_fn, p_mean_var, x, t, model_kwargs=None):
"""
Compute what the p_mean_variance output would have been, should the
model's score function be conditioned by cond_fn.
See condition_mean() for details on cond_fn.
Unlike condition_mean(), this instead uses the conditioning strategy
from Song et al (2020).
"""
alpha_bar = _extract_into_tensor(self.alphas_cumprod, t, x.shape)
eps = self._predict_eps_from_xstart(x, t, p_mean_var["pred_xstart"])
eps = eps - (1 - alpha_bar).sqrt() * cond_fn(
x, self._scale_timesteps(t), **model_kwargs
)
out = p_mean_var.copy()
out["pred_xstart"] = self._predict_xstart_from_eps(x, t, eps)
out["mean"], _, _ = self.q_posterior_mean_variance(
x_start=out["pred_xstart"], x_t=x, t=t
)
return out
DDPM sampling
p_sample은 특정한 timestep t에서 x_t-1을 샘플링하는 함수이다. 위의 p_mean_variance 함수는 mean, variance, log_variance, pred_xstart의 네 가지 값을 리턴한다. 이때 noise와 nonzero_mask를 만드는데, noise는 x와 같은 크기의 가우시안 노이즈, 그리고 nonzero_mask는 t>0일 때만 noise항이 합해지도록 하는 마스크이다.
또한, conditioning이 있을 때는 condition_mean을 이용하여 output의 mean을 수정해 준다. 리턴하는 샘플은 reparametrization trick을 이용해 mean과 variance로 샘플링한 x_t-1이다.
def p_sample(
self,
model,
x,
t,
clip_denoised=True,
denoised_fn=None,
cond_fn=None,
model_kwargs=None,
):
"""
Sample x_{t-1} from the model at the given timestep.
:param model: the model to sample from.
:param x: the current tensor at x_{t-1}.
:param t: the value of t, starting at 0 for the first diffusion step.
:param clip_denoised: if True, clip the x_start prediction to [-1, 1].
:param denoised_fn: if not None, a function which applies to the
x_start prediction before it is used to sample.
:param cond_fn: if not None, this is a gradient function that acts
similarly to the model.
:param model_kwargs: if not None, a dict of extra keyword arguments to
pass to the model. This can be used for conditioning.
:return: a dict containing the following keys:
- 'sample': a random sample from the model.
- 'pred_xstart': a prediction of x_0.
"""
out = self.p_mean_variance(
model,
x,
t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
model_kwargs=model_kwargs,
)
noise = th.randn_like(x)
nonzero_mask = (
(t != 0).float().view(-1, *([1] * (len(x.shape) - 1)))
) # no noise when t == 0
if cond_fn is not None:
out["mean"] = self.condition_mean(
cond_fn, out, x, t, model_kwargs=model_kwargs
)
sample = out["mean"] + nonzero_mask * th.exp(0.5 * out["log_variance"]) * noise
return {"sample": sample, "pred_xstart": out["pred_xstart"]}
p_sample_loop은 gradient update를 하지 않는 모델과 input의 shape, 그리고 noise를 이용해서 sampling한다. p_sample_loop_progressive라는 이터러블에서 sample을 가져와서 이를 final에 저장했다. 아래 메소드를 보면, 샘플링에 핵심이 되는 코드는 p_sample_loop_progressive에 들어있음을 확인할 수 있다.
def p_sample_loop(
self,
model,
shape,
noise=None,
clip_denoised=True,
denoised_fn=None,
cond_fn=None,
model_kwargs=None,
device=None,
progress=False,
):
"""
Generate samples from the model.
:param model: the model module.
:param shape: the shape of the samples, (N, C, H, W).
:param noise: if specified, the noise from the encoder to sample.
Should be of the same shape as `shape`.
:param clip_denoised: if True, clip x_start predictions to [-1, 1].
:param denoised_fn: if not None, a function which applies to the
x_start prediction before it is used to sample.
:param cond_fn: if not None, this is a gradient function that acts
similarly to the model.
:param model_kwargs: if not None, a dict of extra keyword arguments to
pass to the model. This can be used for conditioning.
:param device: if specified, the device to create the samples on.
If not specified, use a model parameter's device.
:param progress: if True, show a tqdm progress bar.
:return: a non-differentiable batch of samples.
"""
final = None
for sample in self.p_sample_loop_progressive(
model,
shape,
noise=noise,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
cond_fn=cond_fn,
model_kwargs=model_kwargs,
device=device,
progress=progress,
):
final = sample
return final["sample"]
본격적인 sampling loop인 p_sample_loop_progressive는 아래와 같은 두 스텝으로 구성된다.
- 입력값 처리 및 세팅 : device를 설정하고, noise를 샘플링의 시작 이미지 (x_T)로 설정한다. 또한 noise가 들어오지 않았다면, shape와 같은 랜덤 noise를 만든다. Default로 False로 설정된 progress 는 tqdm progress bar를 만든다. 즉, progress = True로 하면 progress bar를 볼 수 있다. indices는 num_timesteps에 해당하는 T값에 대한 range가 reverse된 리스트가 들어간다. 즉 T, T-1, ..., 0으로 순환해서 샘플링하기 위함이다.
- 샘플링 루프 : 위에서 정의한 p_sample 코드(-> 'sample', 'pred_start' 두 가지 리턴)를 이용하여 샘플링한다. 루프를 보면 out에 p_sample 결과가 저장되고, out['sample']를 img에 할당하여 새로운 indices의 out 계산에 활용됨을 확인할 수 있다.
def p_sample_loop_progressive(
self,
model,
shape,
noise=None,
clip_denoised=True,
denoised_fn=None,
cond_fn=None,
model_kwargs=None,
device=None,
progress=False,
):
"""
Generate samples from the model and yield intermediate samples from
each timestep of diffusion.
Arguments are the same as p_sample_loop().
Returns a generator over dicts, where each dict is the return value of
p_sample().
"""
if device is None:
device = next(model.parameters()).device
assert isinstance(shape, (tuple, list))
if noise is not None:
img = noise
else:
img = th.randn(*shape, device=device)
indices = list(range(self.num_timesteps))[::-1]
if progress:
# Lazy import so that we don't depend on tqdm.
from tqdm.auto import tqdm
indices = tqdm(indices)
for i in indices:
t = th.tensor([i] * shape[0], device=device)
with th.no_grad():
out = self.p_sample(
model,
img,
t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
cond_fn=cond_fn,
model_kwargs=model_kwargs,
)
yield out
img = out["sample"]
DDIM Sampling
ddim_sample 함수는 위에서 정의한 DDPM에서의 p_sample과 유사한 기능을 한다. 즉 x_t를 받아 output으로 x_t-1(sample)과 x_0 (pred_xstart)을 리턴하는 것이다. p_sample에서는 p_mean_variance를 이용하여 분포 p(x_t | x_t-1)의 mean과 variance를 계산하고, reparametrization trick을 이용해 x_t-1을 샘플링했다면 ddim_sample은 아래 식을 이용하여 샘플링한다. 앞의 두 항이 mean_pred에 들어간다.
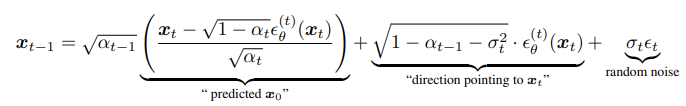
이때 sigma 값은 하이퍼파라미터 eta를 이용하여 아래와 같이 계산된다.
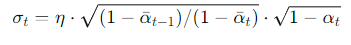
def ddim_sample(
self,
model,
x,
t,
clip_denoised=True,
denoised_fn=None,
cond_fn=None,
model_kwargs=None,
eta=0.0,
):
"""
Sample x_{t-1} from the model using DDIM.
Same usage as p_sample().
"""
out = self.p_mean_variance(
model,
x,
t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
model_kwargs=model_kwargs,
)
if cond_fn is not None:
out = self.condition_score(cond_fn, out, x, t, model_kwargs=model_kwargs)
# Usually our model outputs epsilon, but we re-derive it
# in case we used x_start or x_prev prediction.
eps = self._predict_eps_from_xstart(x, t, out["pred_xstart"])
alpha_bar = _extract_into_tensor(self.alphas_cumprod, t, x.shape)
alpha_bar_prev = _extract_into_tensor(self.alphas_cumprod_prev, t, x.shape)
sigma = (
eta
* th.sqrt((1 - alpha_bar_prev) / (1 - alpha_bar))
* th.sqrt(1 - alpha_bar / alpha_bar_prev)
)
# Equation 12.
noise = th.randn_like(x)
mean_pred = (
out["pred_xstart"] * th.sqrt(alpha_bar_prev)
+ th.sqrt(1 - alpha_bar_prev - sigma ** 2) * eps
)
nonzero_mask = (
(t != 0).float().view(-1, *([1] * (len(x.shape) - 1)))
) # no noise when t == 0
sample = mean_pred + nonzero_mask * sigma * noise
return {"sample": sample, "pred_xstart": out["pred_xstart"]}
Song et al.의 DDIM 과정에서, eta = 0일 경우 sampling 과정이 완전히 deterministic해져 같은 latent라면 반드시 같은 output을 도출한다는 내용이 있었다. 이 원리를 이용하여, x_t가 주어졌을 때 x_t+1을 reverse sampling하는 방법을 생각할 수 있다. 일반적으로 forward diffusion process는 아래와 같은 noising을 따른다.
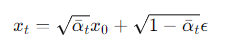
여기서 deterministic 한 과정이라면 x_t를 통해 예측된 x_0 (p_mean_variance가 리턴한 out['pred_xstart']) 을 이용해 epsilon을 계산하고, 이를 다시 x_t+1에 대해 동일한 식을 적용하여 샘플링할 수 있다. 즉, 위 식을 epsilon에 대해 변형하면 아래와 같다.
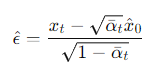
이 epsilon을 이용해서 다시 아래와 같이 샘플링하는 것이다.
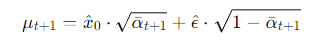
def ddim_reverse_sample(
self,
model,
x,
t,
clip_denoised=True,
denoised_fn=None,
model_kwargs=None,
eta=0.0,
):
"""
Sample x_{t+1} from the model using DDIM reverse ODE.
"""
assert eta == 0.0, "Reverse ODE only for deterministic path"
out = self.p_mean_variance(
model,
x,
t,
clip_denoised=clip_denoised,
denoised_fn=denoised_fn,
model_kwargs=model_kwargs,
)
# Usually our model outputs epsilon, but we re-derive it
# in case we used x_start or x_prev prediction.
eps = (
_extract_into_tensor(self.sqrt_recip_alphas_cumprod, t, x.shape) * x
- out["pred_xstart"]
) / _extract_into_tensor(self.sqrt_recipm1_alphas_cumprod, t, x.shape)
alpha_bar_next = _extract_into_tensor(self.alphas_cumprod_next, t, x.shape)
# Equation 12. reversed
mean_pred = (
out["pred_xstart"] * th.sqrt(alpha_bar_next)
+ th.sqrt(1 - alpha_bar_next) * eps
)
return {"sample": mean_pred, "pred_xstart": out["pred_xstart"]}
DDIM sampling loop은 DDPM의 p_sample_loop와 유사한 기능을 한다. 마찬가지로, 핵심 코드는 iterable인 ddim_sample_loop_progressive 에 들어있음을 확인할 수 있다. 여기서의 ddim_sample과 ddim_sample_loop_progressive 는 DDPM과 너무 유사하므로 리뷰를 생략한다.
Loss 계산
먼저, likelihood-based loss 계산을 위해 losses.py에서 아래와 같이 import 해 주었다.
from .losses import normal_kl, discretized_gaussian_log_likelihood- normal_kl은 두 개의 gaussian distribution의 mean과 logvar를 받아서 KL divergence 를 계산해 준다.
- discretized_gaussian_log_likelihood 는 target image가 목표하는 gaussian distribution으로부터 샘플링될 log likelihood를 계산한다. 이때 target image, mean, log score(표준편차)를 받아서 nat단위(자연로그)로 리턴한다.
_vb_terms_bpd 함수는 output으로 나온 이미지들에 대한 KL 혹은 NLL을 리턴한다. 첫 번째 타임스텝일 때는 NLL,을, 이외에는 아래와 같은 KL이 output에 들어간다. 즉 diffusion posterior와 학습된 sampling 분포 사이의 KLD이다. NLL 계산할 때는 discretized_gaussian_lod_likelihood가 nat 단위로 리턴하므로 bpd (비트, 밑이 2) 단위로 변환해 주었다.
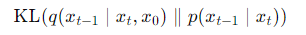
def _vb_terms_bpd(
self, model, x_start, x_t, t, clip_denoised=True, model_kwargs=None
):
"""
Get a term for the variational lower-bound.
The resulting units are bits (rather than nats, as one might expect).
This allows for comparison to other papers.
:return: a dict with the following keys:
- 'output': a shape [N] tensor of NLLs or KLs.
- 'pred_xstart': the x_0 predictions.
"""
true_mean, _, true_log_variance_clipped = self.q_posterior_mean_variance(
x_start=x_start, x_t=x_t, t=t
)
out = self.p_mean_variance(
model, x_t, t, clip_denoised=clip_denoised, model_kwargs=model_kwargs
)
kl = normal_kl(
true_mean, true_log_variance_clipped, out["mean"], out["log_variance"]
)
kl = mean_flat(kl) / np.log(2.0)
decoder_nll = -discretized_gaussian_log_likelihood(
x_start, means=out["mean"], log_scales=0.5 * out["log_variance"]
)
assert decoder_nll.shape == x_start.shape
decoder_nll = mean_flat(decoder_nll) / np.log(2.0)
# At the first timestep return the decoder NLL,
# otherwise return KL(q(x_{t-1}|x_t,x_0) || p(x_{t-1}|x_t))
output = th.where((t == 0), decoder_nll, kl)
return {"output": output, "pred_xstart": out["pred_xstart"]}
training_losses는 하나의 timestep에 대한 model의 loss를 계산한다. 이 함수는 두 가지 종류의 loss를 취급하는데, 모델 argument인 use_kl의 참, 거짓에 따라 아래 두 가지 loss를 사용할 수 있다.
- (RESCALED) KL
- (RESCALED) MSE
이 함수에서 model의 설정 (LossType, ModelMeanType, ModelVarType 등)에 따라 올바른 종류의 loss를 계산한다.
def training_losses(self, model, x_start, t, model_kwargs=None, noise=None):
"""
Compute training losses for a single timestep.
:param model: the model to evaluate loss on.
:param x_start: the [N x C x ...] tensor of inputs.
:param t: a batch of timestep indices.
:param model_kwargs: if not None, a dict of extra keyword arguments to
pass to the model. This can be used for conditioning.
:param noise: if specified, the specific Gaussian noise to try to remove.
:return: a dict with the key "loss" containing a tensor of shape [N].
Some mean or variance settings may also have other keys.
"""
if model_kwargs is None:
model_kwargs = {}
if noise is None:
noise = th.randn_like(x_start)
x_t = self.q_sample(x_start, t, noise=noise)
terms = {}
if self.loss_type == LossType.KL or self.loss_type == LossType.RESCALED_KL:
terms["loss"] = self._vb_terms_bpd(
model=model,
x_start=x_start,
x_t=x_t,
t=t,
clip_denoised=False,
model_kwargs=model_kwargs,
)["output"]
if self.loss_type == LossType.RESCALED_KL:
terms["loss"] *= self.num_timesteps
elif self.loss_type == LossType.MSE or self.loss_type == LossType.RESCALED_MSE:
model_output = model(x_t, self._scale_timesteps(t), **model_kwargs)
if self.model_var_type in [
ModelVarType.LEARNED,
ModelVarType.LEARNED_RANGE,
]:
B, C = x_t.shape[:2]
assert model_output.shape == (B, C * 2, *x_t.shape[2:])
model_output, model_var_values = th.split(model_output, C, dim=1)
# Learn the variance using the variational bound, but don't let
# it affect our mean prediction.
frozen_out = th.cat([model_output.detach(), model_var_values], dim=1)
terms["vb"] = self._vb_terms_bpd(
model=lambda *args, r=frozen_out: r,
x_start=x_start,
x_t=x_t,
t=t,
clip_denoised=False,
)["output"]
if self.loss_type == LossType.RESCALED_MSE:
# Divide by 1000 for equivalence with initial implementation.
# Without a factor of 1/1000, the VB term hurts the MSE term.
terms["vb"] *= self.num_timesteps / 1000.0
target = {
ModelMeanType.PREVIOUS_X: self.q_posterior_mean_variance(
x_start=x_start, x_t=x_t, t=t
)[0],
ModelMeanType.START_X: x_start,
ModelMeanType.EPSILON: noise,
}[self.model_mean_type]
assert model_output.shape == target.shape == x_start.shape
terms["mse"] = mean_flat((target - model_output) ** 2)
if "vb" in terms:
terms["loss"] = terms["mse"] + terms["vb"]
else:
terms["loss"] = terms["mse"]
else:
raise NotImplementedError(self.loss_type)
return terms
'머신러닝&딥러닝 > 생성모델' 카테고리의 다른 글
| cGAN (2014)의 간단한 오버뷰 (0) | 2025.01.22 |
|---|---|
| VAE latent는 어떻게 생겼을까? (feat. PCA) (0) | 2024.08.14 |
| Classifier Guidance 논문리뷰 (Diffusion Models Beat GANs on Image Synthesis, 2021) (0) | 2024.08.14 |
| DDIM 논문 리뷰 - 샘플링 가속과 consistency (0) | 2024.08.14 |
| DDPM pytorch 코드분석 (0) | 2024.08.13 |