2024. 8. 14. 03:26ㆍ머신러닝&딥러닝/생성모델
본 포스팅에서는 DDPM의 일반화 버전인 DDIM을 리뷰하려고 한다. DDPM과 무엇이 어떻게 다른 걸까?
Introduction
Generative model의 역사
GAN은 VAE(2013), autoregressive model(2016), normalizing flow(2015) 보다 나은 sampling quality를 가지지만, training stability가 낮고 데이터 분포의 mode를 제대로 커버하지 못할 수 있다.
최근 생성모델은 score based network(NCSN)이나 iterative model(DDPM)과 같은 모델이 좋은 성능을 보이고 있으나, DDPM의 치명적인 단점은 샘플링 속도가 매우 느리다는 것이다.
DDIM(Denoising Diffusion Implicit Model)은 GAN과 DDPM의 효율성을 상호보완하기 위해 만들어진 모델이다. DDIM과 DDPM의 가장 큰 차이는 DDPM은 markovian이지만 DDIM은 non-markovian이라는 점이다. 즉, DDPM에서 x_t는 x_t-1에 의해서만 결정되지만, DDIM에서는 x_t-1과 x_0에 의해 결정된다.

이는 더 짧은 Markov chain을 만들어 sampling step을 줄일 수 있다. 또한, DDPM에 비해 나은 generation quality를 보인다. 마지막으로 DDIM은 "consistency"라는 속성이 있는데, 이는 동일한 latent 에서 다양한 길이의 markov chain으로 generation한 이미지는 동일한 high-level feature를 가진다는 점이다.
Background

DDPM loss를 간단히 소개하였고, loss는 위와 같이 식을 변형할 수 있음을 설명하였다.
Non-Markovian forward process
DDIM의 Non-Markovian forward process는 DDPM과 달리 sigma라는 인자가 사용된다. Sigma가 왜 붙는지에 대해 결론부터 이야기하면, noising process의 랜덤한 정도를 조절한다. sigma가 0이면, x_0과 x_t를 알 수 있다면 x_t-1이 하나로 정해져 모델이 결정론적이 된다.
아래와 같은 식으로 정의되는 DDPM inference distribution과 달리,

DDIM의 inference distribution은 아래와 같다.

우변에 있는 두 식 q(x_T | x_0)과 q(x_t-1 | x_t, x_o)은 아래와 같은 분포를 따르도록 정의된다.


이렇게 설정하면, 모든 t에 대해 아래가 만족된다 (증명은 appendix 참고..)

DDIM의 forward process는 x_0과 x_t-1로 x_t를 찾는 과정이며, 이는 베이즈 정리를 이용하여 아래와 같이 적을 수 있다.

Generative process & Unified Variational Inference Objective
DDIM에서는 x_t가 주어졌을 때, p(x_t-1|x_t)가 q(x_t-1 | x_t, x_0)를 이용하여 x0을 먼저 예측하고 x_t-1을 샘플링한다. 즉, 아래 두 스텝으로 denoising이 되는 것이다.
- x_t로 x_0 예측
- x_t와 예측한 x_0으로 x_t-1 추정 (q)
첫 번째 과정은 아래 식으로 나태낼 수 있다. 즉 f(x_t)는 예측된 x_0값이 되는 것이다.

두 번째 과정은 아래 식으로 나타낼 수 있다.

Sampling
DDIM에서는 x_t에서 아래와 같은 식으로 x_t-1을 샘플링한다.

위에서 설명한 것처럼, x_t에서 x_0을 예측하고, 이것으로 x_t-1 을 추정하는 구조인데, 여기에 랜덤성을 더하기 위해 sigma 변수를 추가한다. 즉 sigma = 0이면 predicted x_0으로 곧바로 x_t-1이 정해지므로 결정론적이다. 언뜻 보기에는 1 step의 denoising 과정이 DDPM보다 복잡해 보이는데, 어떻게 샘플링을 가속할까?
Accelerated Generation
DDIM에서는 q(x_t | x_0)이 고정되어 있다면 forward process에서 어떻게 노이즈를 주입하든 특정 시점 t에서의 x_t는 항상 동일하게 결정된다. 이것이 중요한 아이디어인데, DDPM에서는 [1, 2, ..., T]의 타임스텝 모두 noising하고, 반대로 denoising할 때도 하나씩 해야 했지만 DDIM에서는 그렇지 않다. 즉 전체 타임스텝 [1, 2, ... T]의 길이 S짜리 부분수열 tau를 생각하고, 그 안에서만 noising-denoising을 수행하면 된다.

즉 tau가 [1, 3]이면 위와 같이 x_2를 건너뛸 수 있는 것이다. 이 tau를 뒤집은 것이 샘플링 순서가 되며, 이를 sampling trajectory라고 한다.
Experiments
DDIM은 DDPM보다 훨씬 빠른 속도로 generation 가능하며, x_T가 고정되어 있다면 trajectory에 상관없이 유사한 high level feature를 보존할 수 있다. 따라서, latent에서의 interpolation이 가능하다.
본 논문에서는 동일하게 train된 모델을, trajectory tau를 바꿔 가면서 실험했다. 또한 sigma는 아래와 같이 결정된다.

이때 앞에 붙는 eta는 직접 조절 가능한 하이퍼파라미터로, eta=0일 때 DDPM과 완전히 같아진다. 또한 eta=0일 때 DDIM이 된다.
먼저, 같은 S값에 대해 DDPM과 DDIM 중 DDIM이 더 낮은 FID를 보여 성능이 좋았다. 또한, S값이 커질수록 FID는 작아졌는데, 이는 샘플링 효율과 이미지의 퀄리티 사이에는 trade-off가 있음을 시사한다.

아래 이미지를 보면 S = 10일 때와 S=100일 때 이미지의 퀄리티가 다름을 확인할 수 있다.

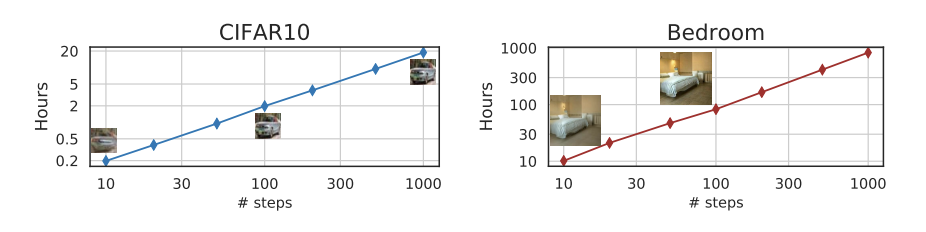
아래 그래프를 보면 trajectory를 조정하여 샘플링 시간을 크게 절약할 수 있는 것을 확인할 수 있다.
또한, 같은 latent x_T에서 샘플링된 이미지는, trajectory에 상관없이 동일한 high level feature를 갖는 consistency를 보였다.

x_T에 high level feature 특징이 인코딩된다는 이러한 consistency 특성 때문에, interpolation을 적용했을 때 semantic 정보를 유지하는 interpolation을 latent단에서 수행할 수 있다.

반면, DDPM에서의 interpolation은 latent에서의 interpolation이 아니다. 실제 source이미지를 linear interpolation한 뒤, 노이즈를 조금 첨가 후 denoising한 것이다.

이러한 특성 때문에, DDIM에서는 latent space에서의 reconstruction 또한 높은 성능으로 가능하다.

'머신러닝&딥러닝 > 생성모델' 카테고리의 다른 글
| VAE latent는 어떻게 생겼을까? (feat. PCA) (0) | 2024.08.14 |
|---|---|
| Classifier Guidance 논문리뷰 (Diffusion Models Beat GANs on Image Synthesis, 2021) (0) | 2024.08.14 |
| DDPM pytorch 코드분석 (0) | 2024.08.13 |
| AnoDDPM 논문 리뷰 (AnoDDPM: Anomaly Detection with Denoising Diffusion Probabilistic Models using Simplex Noise) (0) | 2024.08.06 |
| U-ViT 논문 리뷰(All are Worth Words: A ViT Backbone for Diffusion Models, 2022) (0) | 2024.07.29 |