2024. 3. 5. 00:05ㆍ머신러닝&딥러닝/생성모델
정보 엔트로피(Information Entropy)
정보 엔트로피를 이해하기 위해, 먼저 정보량을 정의하자. 사막에 여행을 갔다고 생각하자. 현지인에게 "내일의 날씨는 어떤가요?"라고 물어봤을 때 나올 수 있는 두 개의 대답을 생각해 보자.
- 내일은 해가 쨍쨍할 예정입니다.
- 내일은 비가 올 예정입니다.
사막에서 해가 쨍쨍한 것은 어찌 보면 당연한 일로, 확률이 매우 높다. 반면 비가 오는 일은 아주 드문 일로 확률이 낮다. 직관적으로 둘 중 어떤 대답에 더 많은 정보량이 들어 있는가? 당연히 후자일 것이다. 정보량은 일어날 확률이 드문 일일수록 커진다. 따라서 어떤 사건 X에 대해 정보량은 P(X)에 반비례한다.
조금 더 정확하게는, X의 정보량 I(X)를 아래와 같이 정의할 수 있다. (로그의 밑 b는 상황에 따라 2, 10, e의 값을 사용한다)

마이너스 로그 함수는 우하향하는 곡선이므로, P(X)가 증가할 때 I(X)가 감소하는 관계를 나타낼 수 있다. 그런데 왜 수많은 우하향하는 함수 중 마이너스 로그 함수일까? 독립인 두 사건 X와 Y가 발생할 때의 정보량은, 두 사건이 각각 일어날 때의 정보량의 합과 동일해야 하기 때문이다. 독립인 두 사건 X와 Y가 동시에 발생할 확률은 각각의 사건이 발생할 확률의 곱과 같으므로, 확률에서의 곱이 정보량에서의 합으로 변환되어야 한다. 따라서 로그 함수가 적용되는 것이다.

평균 정보량(Shannon's Entropy)
평균 정보량 H(X)은 확률변수 X에 대하여 X의 원소들의 평균 엔트로피이다. 즉, 이산확률변수일 때는

와 같이 나타낼 수 있고, 연속확률변수일 때는

와 같이 나타낼 수 있다. 이때 p(x)는 확률밀도함수(PDF)이다.

예를 들어, 동전을 던지는 상황을 생각해 보자. 확률변수 X는 앞면 H가 나올 확률 0.5, 뒷면 T가 나올 확률 0.5인 이산확률분포를 따를 것이다. 이때 평균 정보량 H(X)는

와 같이 된다. 그런데, 이번에는 동전이 구부러져 앞면 H가 나올 확률이 0.25, 뒷면 T가 나올 확률 0.75인 분포라고 해 보자. 그러면 평균 정보량 H(X)는
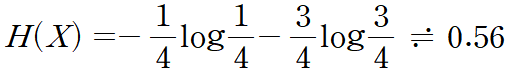
이다. log2 = 0.3010이므로, 구부러진 동전을 던질 때의 정보 엔트로피가 더 큰 것을 알 수 있다.
Cross Entropy
Binary Cross Entropy(BCE)
이진 분류(Binary Classification)란, 정답의 카테고리가 둘 중 하나인 분류를 말한다. 이전 포스팅에서부터 등장하는 "스팸 메일 분류기"를 다시 예로 들 때, 어떤 메일을 분류 결과는 "스팸 메일"과 "스팸 메일 아님"의 두 가지로만 나타나므로 이것은 이진 분류이다. 메일이 왔을 때, 분류기는 이 메일이 스팸 메일을 확률을 측정한다. 그 확률이 0.5 이상이면, 스팸 메일이고, 0.5보다 낮으면 스팸 매일이 아닌 것으로 분류한다.
BCE(Binary Cross Entropy)는 이러한 이진 분류 문제에서 사용되는 loss function이다. 스팸 메일을 1, 스팸 메일이 아닌 메일을 0이라고 정답을 정해 놓고, 분류기가 출력한 스팸 메일일 확률을 y_hat이라고 하자. 그러면 BCE를 다음과 같이 정의할 수 있다.

정답이 1인 경우, 우변의 두번째 항이 소거되므로 첫 번째 항만 살아남는다. 이때 y_hat 값이 1에 가까울수록 BCE값은 0에 가까워질 것이다. 정답이 0인 경우, 우변의 첫 번째 항이 소거된다. 이때 y_hat 값이 0에 가까울수록 BCE는 0에 가까워진다. 따라서, 레이블링된 정답과 실제 분류기를 통해 예측한 확률이 유사할수록 함숫값이 작아지는 loss function 형태를 띤다. 이를 N개의 데이터로 확장한다면, 전체의 BCE는 각 데이터의 BCE값의 평균이 된다.

Cross Entropy는 BCE에서 0 또는 1로 분류되었던 정답을, "정답 분포"로 바꾸어주기만 하면 된다. 즉, 머신이 내놓은 예측 모델링의 분포를 q(x), 정답 분포를 p(x)라고 할 때, Cross entropy는 아래와 같이 정의된다.

쿨백 - 라이블러 발산 (Kullback-Leibler Divergence, KL Divergence)
머신러닝의 목적은, 예측 모델링의 분포 q(x)를 정답 분포 p(x)에 최대한 근사하는 것이다. 이를 위해, 정답 분포 P와, cross entropy 의 차이를 계산한 것이 쿨백 - 라이블러 발산이다.

KL(P||Q)에서 Q가 예측 분포, P가 정답 분포이므로, 두 분포가 일치하면 위 식에서 로그 안의 값이 1이 나와 KL divergence 값이 0이 나온다. KL divergence는 두 분포 사이의 정보 손실량으로 볼 수도 있다.
KL divergence는 아래와 같은 특징을 가진다.
- KL divergence는 비음수성(Non-negativity)를 가진다. 즉, KL(P||Q)는 항상 0 이상이며, P = Q일 때 0이 된다.
- KL divergence는 비대칭성(Asymmetry)를 가진다. 즉, KL(P||Q)는 KL(Q||P)와 다르다. 이는 위 식을 통해 쉽게 할 수 있다. 이러한 이유로 KL divergence는 거리 함수가 아니다. 그래서 distance가 아니라 divergence라는 용어를 쓰는 것이다.
'머신러닝&딥러닝 > 생성모델' 카테고리의 다른 글
| 생성 모델로 만든 이미지의 평가 방법 (S.Azizi 2023 논문 리뷰) (1) | 2024.04.15 |
|---|---|
| DDPM을 통한 이미지 생성 및 보간 (J. Ho 2020 논문 리뷰) (1) | 2024.03.22 |
| Variational Auto-Encoder (Kingma, 2013 논문 리뷰) (0) | 2024.03.06 |
| ML(Maximum Likelihood), MAP(Maximum A Posteriori) 추정 (0) | 2024.03.04 |
| 베이즈 결정 이론(Bayesian Decision Theorem) (1) | 2024.03.03 |