2024. 2. 27. 23:54ㆍ머신러닝&딥러닝/영상처리
공간 연산(Spatial Operation)은 세 가지 범주로 나뉜다.
- 단일 픽셀 연산(Single Pixel Operation)
- 이웃 연산(Neighborhood Operation)
- 기하적 공간 변환(Geometrical Spatial Operation)
오늘 포스팅에서는 각 범주의 개념과 예시를 살펴보고, 기하적 공간 변환의 예시인 영상 보간법(interpolation)에 대해 알아보고자 한다. 이미지는 Digital Image Processing 4th ed. (Rafael C. Gonzalez et al.)을 참고하였다.

단일 픽셀 연산(Single Pixel Operation)
본 포스팅에서는 RGB 영상이 아닌 grayscale 영상에 관해 알아보고자 한다. 그러면 각 pixel (x, y)에 관하여, 그 pixel의 intensity z 까지 합친 3차원 벡터 (x, y, z)를 생각할 수 있다.
Single pixel operation은 단일 픽셀의 intensity z에 어떤 transformation T를 적용하여 새로운 픽셀 변수 s에 mapping 하는 것을 말한다.

예를 들어, 0~255의 intensity를 가지는 영상에서 T를 다음과 같이 s = 255-z로 잡자.

이러한 single pixel operation은 intensity의 "반전"을 만든다.
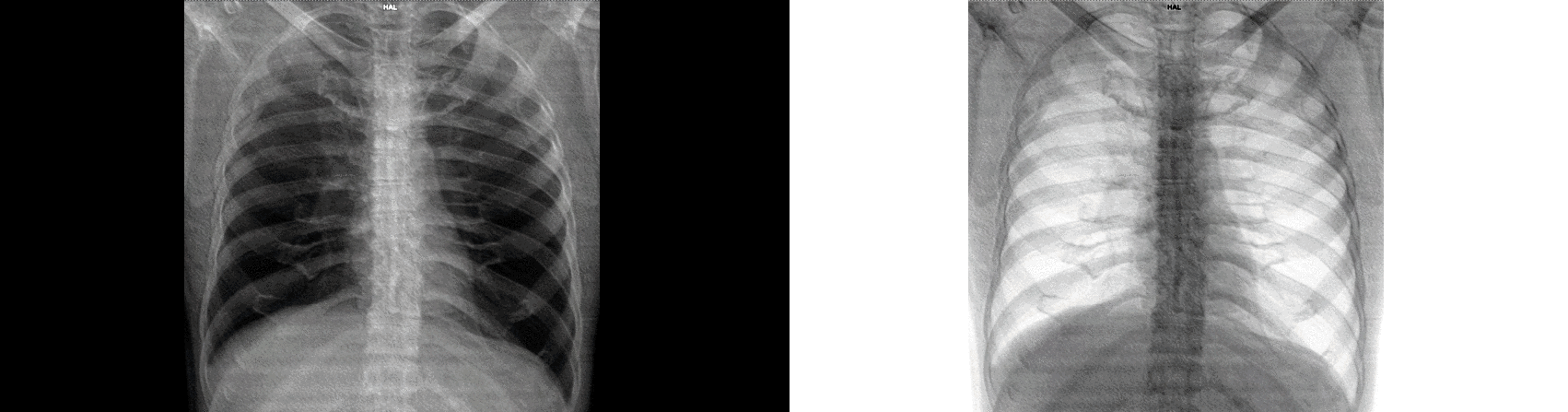
이웃 연산(Neighborhood Operation)
m x n 직사각형 안에 속한 pixel neighborhood에 속하는 pixel 집합을 Sxy라고 하자. Neighborhood operation은 이 집합 전체에 적용되는 연산을 말한다.

예를 들어, 위와 같은 식을 적용하면 g(x,y)에는 직사각형의 픽셀의 intensity 값의 평균이 저장된다. 위와 같은 연산을 averaging function이라고 한다. Averaging function을 적용하면,

위 그림과 같이 blur 처리를 할 수 있다. 이때 직사각형의 크기 m x n이 커진다면 blur의 정도는 더 심해질 것이다.
기하적 공간 변환(Geometrical Spatial Operation)
Geometrical Spatial Operation은 확대, 축소, 회전 등 이미지에 규칙을 따르는 조작을 가하는 변환을 말한다. 이러한 조작을 가하는 데는 변환행렬(transformation matrix) T가 들어간다.

픽셀 좌표는 위와 같이 변환되며,

동일한 intensity를 유지하고자 한다면 위와 같은 matrix A가 곱해진다.
가하고 싶은 변환에 따라 다른 종류의 변환행렬을 적용하면 된다.
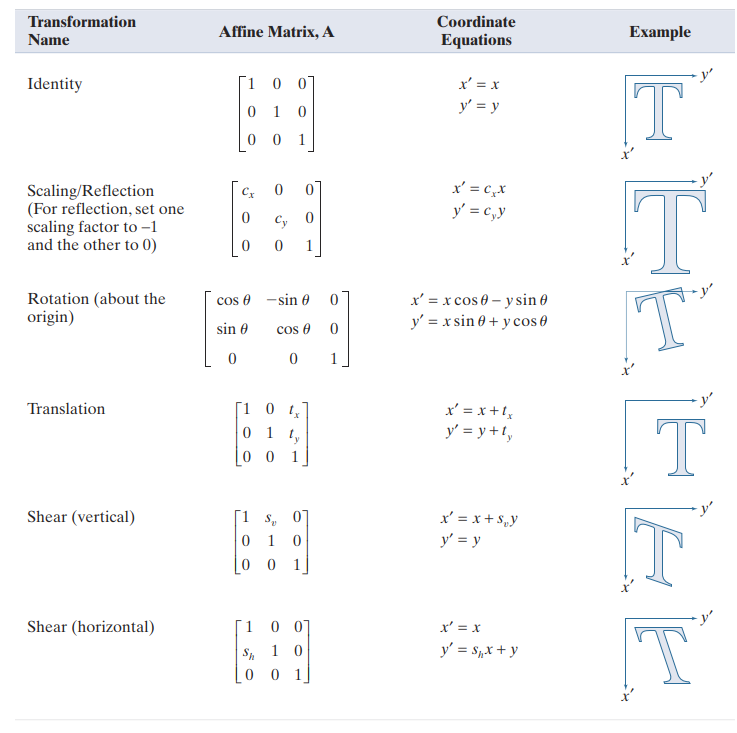
여기에서 문제가 생기는 것은, pixel의 x좌표와 y좌표는 integer이지만 이미지 회전 시 cos, sin 값은 float이므로 정확히 매칭이 이루어지지 않는다. 회전 이외에도 원래 이미지에서 loss가 생기거나 추가해야 할 pixel들이 생기는 문제가 발생하는데, 여기에서 사용하는 해결책이 이미지의 보간(interpolation)이다.

이미지 보간법(interpolation)
이미지 보간법은 회전 등 geometrical spatial operation 상황에서, (x, y)와 (x', y')간에 완벽한 매칭이 발생하지 않는 경우를 보완하는 방법이다.
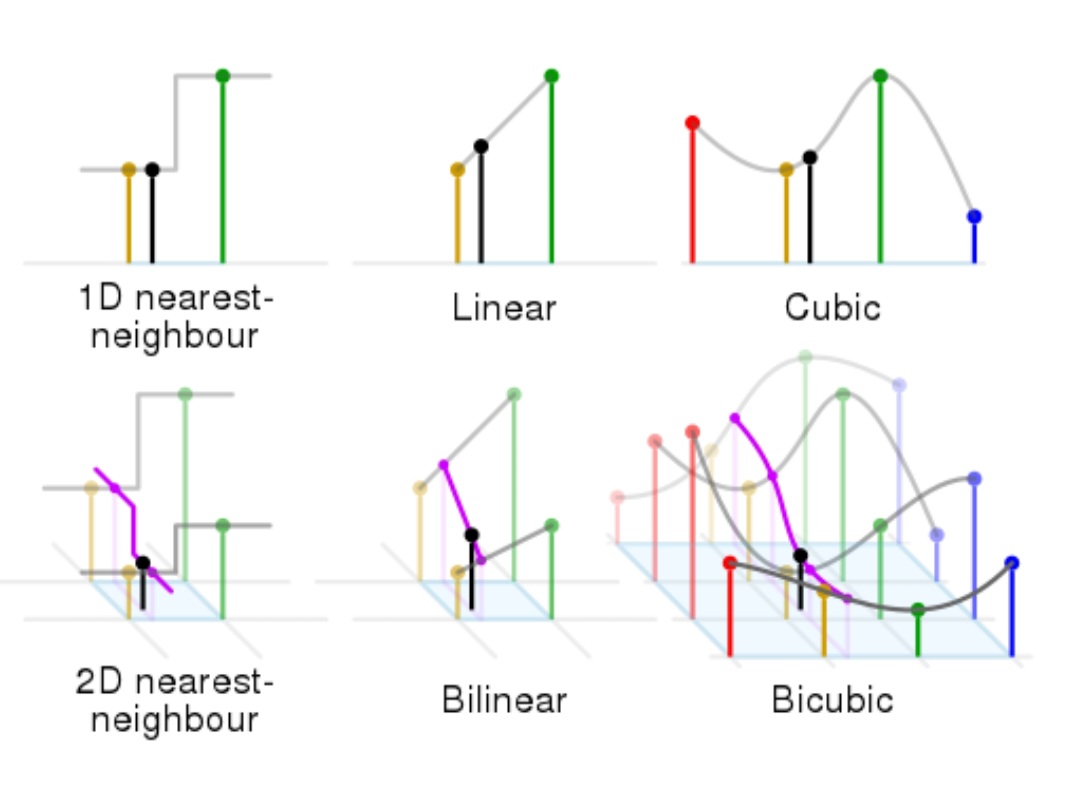
1. Nearest-neighbor interpolation
가장 가까운 픽셀 값을 새 픽셀에 할당한다. Mspaint(그림판)이 이 방식의 보간법을 사용한다. 그림판을 사용해본 사람이라면 알겠지만, 해상도의 손실이 상당히 발생한다. 대신 알고리즘이 간단하다는 장점이 있다.
2. Bilinear interpolation
가장 가까운 4개 픽셀의 가중 평균을 새 픽셀에 할당한다. 구체적으로, 4개의 픽셀을 2개씩 나누어 가중치평균을 낸 후 두 값을 다시 가중치평균한다. Nearest neighbor보다는 나은 방법이지만, 여전히 일부 이미지 손실이 생긴다.
3. Bicubic interpolation
16개의 가장 가까운 픽셀의 거리에 따른 가중 평균을 새 픽셀에 할당한다. 일반적으로는 4개씩 묶어 4개의 가중치평균값을 만들고 다시 가중치평균한다.
4. Spline interpolation
데이터 간의 연속함수를 추정하여, 이미지 전체를 3차원 텐서로 읽고 특정 구간에 맞는 다항함수를 생성한다. 가장 헤비한 방법이지만, 이미지 손실이 가장 적다.
'머신러닝&딥러닝 > 영상처리' 카테고리의 다른 글
| 블러(blur)처리와 선명화(sharpening)처리 (0) | 2024.03.11 |
|---|---|
| MNIST 데이터셋에 대하여 (0) | 2024.03.10 |
| Medical Data에서 시간/공간 영역과 주파수 영역 (1) | 2024.03.08 |