2024. 4. 20. 21:29ㆍCS/자료구조
* 본 글은 [윤성우의 열혈 자료구조 - C언어를 이용한 자료구조 학습서] 를 바탕으로 작성하였습니다.
5. 병합 정렬(Merge Sort)
병합 정렬은 divide and conquer라는 알고리즘에 의해 근거하였다. 16개의 데이터를 정렬한다고 하면, 8개짜리 2개로 나눠서 정렬하고 합치는 것이 더 효율적이라는 것이다. 즉, 8개를 다시 4개로, 4개를 다시 2개로 ... 재귀적으로 가장 작은 단위까지 정렬할 데이터를 쪼개면, if문만으로 정렬이 가능한 것이다. 그리고 이를 합쳐 가며 하나로 만들면 된다.
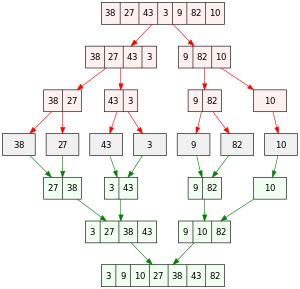
병합 정렬은 구현이 조금 까다롭다. 먼저, MergeSort 함수는 정렬 대상이 되는 데이터의 개수 정보가 아닌 정렬 대상의 범위 정보를 전달해야 한다. 정렬 대상을 계속 쪼개 가면서 진행할 것이기 때문이다. 그래서 정렬 범위를 left, right index로 받아오고, 재귀적으로 함수를 작성해야 한다. 먼저, MergeSort는 아래와 같이 쓸 수 있다.
void MergeSort(int arr[], int left, int right)
{
int mid;
if(left < right)
{
mid = (left+right) / 2;
MergeSort(arr, left, mid);
MergeSort(arr, mid+1, right);
MergeTwoArea(arr, left, mid, right);
}
}
left가 right보다 왼쪽에 있으면 mid를 기준으로 두 개의 배열로 쪼개고, 각각 정렬한 뒤, MergeTwoArea로 두개를 합치는 것이다. 이제 MergeTwoArea를 구현하자. MergeTwoArea는 두 배열의 정렬된 결과를 담을 배열인 sortArr를 malloc 함수로 저장하는 것으로 시작한다. 그리고 while문으로 병합할 두 영역의 데이터를 비교하여 순서대로 sortArr에 하나씩 옮겨 저장한다. (가위바위보 팀전과 비슷하다!!) 한쪽 배열이 모두 sortArr로 옮겨졌다면 나머지 배열의 남은 데이터는 그대로 옮겨오면 된다.
void MergeTwoArea(int arr[], int left, int mid, int right)
{
int fIdx = left;
int rIdx = mid+1;
int i;
int * sortArr = (int*)malloc(sizeof(int)*(right+1));
int sIdx = left;
while(fIdx<=mid && rIdx<=right)
{
if(arr[fIdx] <= arr[rIdx])
sortArr[sIdx] = arr[fIdx++];
else
sortArr[sIdx] = arr[rIdx++];
sIdx++;
}
if(fIdx > mid)
{
for(i=rIdx; i<=right; i++, sIdx++)
sortArr[sIdx] = arr[i];
}
else
{
for(i=fIdx; i<=mid; i++, sIdx++)
sortArr[sIdx] = arr[i];
}
for(i=left; i<=right; i++)
arr[i] = sortArr[i];
free(sortArr);
}
마지막으로는 sortArr를 arr로 다시 옮겨주고, sortArr는 free해준다.
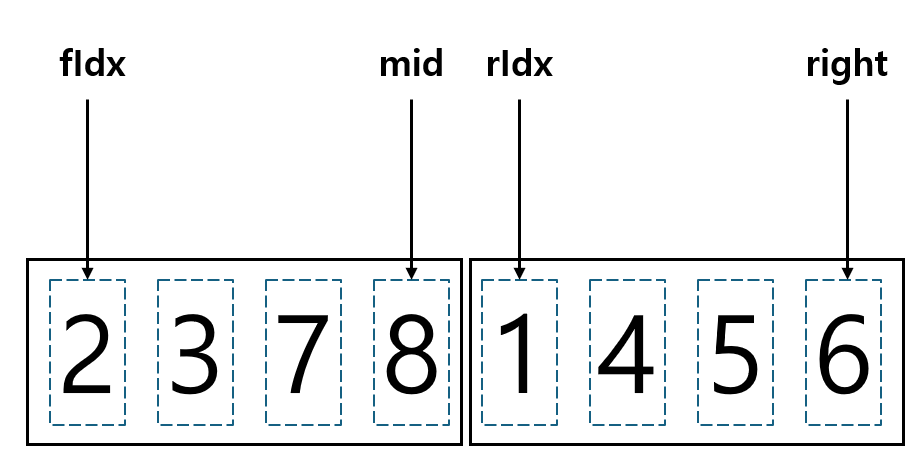
여기서 fIdx는 첫 번째 배열의 첫 번째 위치, rIdx는 두 번째 배열의 첫 번째 위치를 나타내는데, while문의 반복조건 fIdx<=mid && rIdx<=right는 두 배열 모두 남은 데이터가 있음을 의미한다. 그림으로 나타내면 아래와 같은데, 첫 번째와 두 번째 배열에서 하나씩 sortArr로 옮겨질 때마다 fIdx 혹은 rIdx가 오른쪽으로 한 칸씩 옮겨지는 것이다.
병합 정렬의 성능
병합 정렬의 주요한 비교 혹은 이동 연산은 MergeTwoArea 함수를 기준으로 계산한다. n개짜리 데이터셋에서, m/2 길이의 배열들을 합쳐 m짜리 배열을 만드는 것은 최대 n번의 비교연산이 필요하다. 또한, 이러한 "병합"의 횟수는 log_2 n 번 필요하다. 따라서, 병합 정렬의 비교연산을 기준으로 한 성능은 O(nlogn)이다.
또한, 이동 연산은 임시 배열인 sortArr에 데이터를 병합하는 과정과 sortArr의 데이터를 원래 arr로 옮기는 과정에서 필요하므로, 각 상황에서 필요한 이동연산의 횟수는 비교연산의 횟수의 두 배이다. 따하서, 이동 연산을 기준으로 한 성능은 O(nlogn)이다.
6. 퀵 정렬(Quick Sort)
퀵 정렬도 병합 정렬과 마찬가지로 divide and conquer 알고리즘에 의해 만들어졌다. 퀵 정렬의 알고리즘을 그림을 통해 살펴보자.

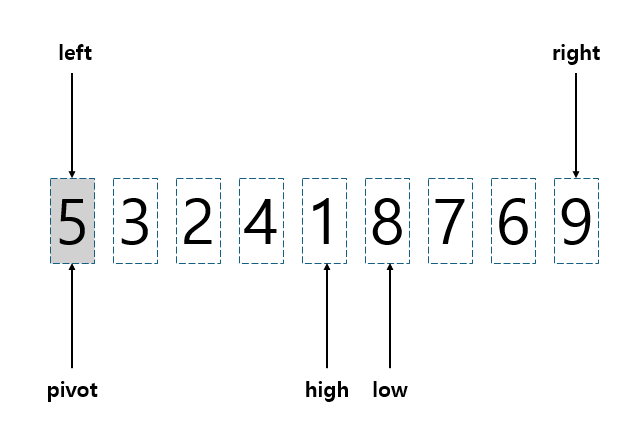
먼저, 가장 왼쪽의 수를 pivot으로 잡자. (가장 오른쪽으로 잡아도 상관없다.) 먼저 low와 high부터 보자.
- low: pivot을 제외하고 가장 왼쪽에 위치한 칸
- high: pivot을 제외하고 가장 오른쪽에 위치한 칸
low는 한 칸씩 오른쪽으로 이동하며 최초로 pivot보다 큰 값을 만났을 때 멈추고, high는 한 칸씩 왼쪽으로 이동하며 최초로 pivot보다 작은 값을 만났을 때 멈춘다.

그 후, 두 칸에 있는 데이터를 바꾼 뒤 다시 low와 high를 이동시킨다.

이 과정을 반복하다 보면, high가 low보다 왼쪽에 위치하게 되는 순간이 온다.
그러면 pivot과 high에 들어있는 데이터를 서로 바꾼다. 이제, 원래 pivot 이었던 "5"를 기준으로, 5의 왼쪽에는 5보다 작은 수들만, 그리고 5의 오른쪽에는 5보다 큰 수들만 놓이게 된다. 그러면 정렬할 배열이 두 부분으로 쪼개진 것과 같다. 이제, left와 right를 같은 방법으로 잡고 이제까지의 과정을 반복하면 된다.
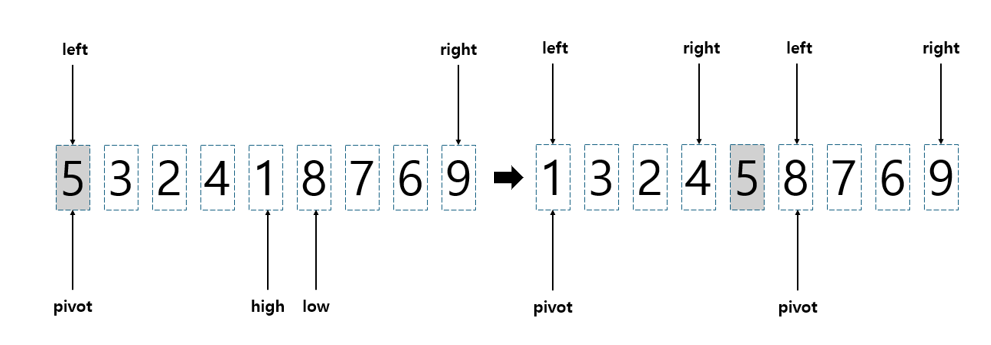
먼저 두 개의 칸에 놓인 데이터를 바꾸는 Swap 함수를 정의하자.
void Swap(int arr[], int idx1, int idx2)
{
int temp = arr[idx1];
arr[idx1] = arr[idx2];
arr[idx2] = temp;
}
다음으로 정의할 함수는, pivot이 제자리를 찾았을 때, 인덱스 값을 리턴하는 Partition 함수이다. pivot 변수에는 변수 값 자체가 들어가지만, low와 high에는 인덱스값이 들어간다. 그리고 while문에 따라, low를 먼저 쭉 올리고, high를 다음으로 쭉 내린다.
int Partition(int arr[], int left, int right)
{
int pivot = arr[left];
int low = left+1;
int high = right;
while(low <= high)
{
while(pivot > arr[low])
low++;
while(pivot < arr[high])
high--;
if(low <= high)
Swap(arr, low, high);
Swap(arr, left, high);
return high;
}
이 함수를 이용해, QuickSort를 아래와 같이 재귀적으로 구현할 수 있다.
void QuickSort(int arr[], int left, int right)
{
if(left <= right)
{
int pivot = Partition(arr, left, right);
QuickSort(arr, left, pivot-1);
QuickSort(arr, pivot+1, right);
}
}
퀵 정렬의 성능
먼저, pivot이 제자리를 찾아가는 과정의 비교연산 횟수는 n-1인데, 그냥 n으로 취급할 수 있다. 따라서, 평균적인 경우에는 둘로 나뉘는 횟수가 log_2 n이므로, 이때 성능은 O(nlogn)이 된다. 그러나, 최악의 상황은 pivot으로 극단적인 값이 오는 경우이다. 예를 들어, 데이터가 이미 정렬되어 있는 경우, 첫 pivot은 1, 둘째는 2, ...와 같이 되기 때문에 둘로 나누는 횟수가 n이 된다. 즉, 성능은 O(n^2)가 되는 것이다. 그러나, 일반적인 경우의 성능 O(nlogn)이 같은 시간복잡도를 가지고 있는 다른 알고리즘에 비해 우수하다는 특징이 있다.
7. 기수 정렬(Radix Sort)
기수 정렬은 앞선 알고리즘과 달리, 비교연산을 하지 않는 알고리즘이다. 또한, 정렬 알고리즘의 이론상 성능의 한계는 O(nlogn)인데, 기수 정렬은 이 한계를 넘어설 수 있는 유일한 알고리즘이다. 단, 적용할 수 있는 데이터의 종류가 제한이 되어 있는데, 바로 데이터의 길이가 같은 데이터만 정렬할 수 있고 길이가 다르면 정렬할 수 없다는 것이다. (정렬이 가능하더라도, 더 비효율적일 수도 있다.)
기수란, 데이터를 구성하는 기본 요소로, 십진수의 경우 0~9의 숫자를 말하며, 영단어의 경우 아스키 코드가 될 수 있다. 예를 들어, 134, 224, 232, 122를 마지막 자리를 기준으로 정렬한다고 할 때, 모든 수가 0~5안에 있으므로, 다섯 개의 버킷을 잡고 아래와 같이 정렬할 수 있다. 또한, 첫 자리나 두 번째 자리를 기준으로 정렬한다고 해도, 같은 버킷 집합을 사용할 수 있다.

이제, 마지막 자리를 기준으로 정렬한 배열을 같은 버킷 집합을 이용하여 두 번째 자리를 기준으로 다시 정렬하고, 이 결과를 첫 번째 자리를 기준을 자리를 기준으로 다시 반복하면 정렬이 완료된다. 즉, 한 문장으로 요약하면 아래와 같다.
가장 중요도가 낮은 자리부터 시작하여 기수를 기준으로 정렬하고,
그 결과를 자리의 중요도를 하나씩 올려 가며 정렬한다.
이를 LSD(Least Significant Digit)부터 정렬한다고 하여 LSD 기수 정렬이라고 한다. 이와 반대로, 가장 높은 자리 MSD(Most Significant Digit)부터 정렬하는 MSD 기수 정렬도 있다. LSD 기수정렬은 가장 마지막에 가장 중요한 일을 하기 때문에 마지막 결과가 최종 정렬 결과가 되지만, MSD 기수 정렬은 중간에 정렬이 완료될 수도 있다. 즉, 성능적인 이점이 있을 수 있으나, 모든 데이터가 일관된 과정을 거쳐 정렬되지 않을수도 있다는 단점이 있다. 예를 들어, 232와 224의 선후를 판단할 때, 둘째 자리를 비교하면 232가 크지만 셋째 자리를 비교하면 224가 크기 때문에, 최종 정렬에서는 224가 더 뒤에 위치하는 잘못된 결과가 나타난다. 따라서, 중간에 데이터를 점검하는 알고리즘을 넣어야 하기 때문에 성능적인 이점이 줄어들 수 있다. 따라서, 일반적으로 기수 정렬이라고 하면 LSD 기수 정렬을 말한다.
여기서 버킷은 구조가 큐에 해당하기 때문에, 연결 리스트를 기반으로 한 큐로 아래와 같이 구현할 수 있다.
void RadixSort(int arr[], int num, int maxLen)
{
Queue buckets[BUCKET_NUM];
int bi;
int pos;
int di;
int divfac = 1;
int radix;
for(bi=0; bi<BUCKET_NUM; bi++)
QueueInit(&buckets[bi]);
for(pos=0; pos<maxLen; pos++)
{
for(di=0; di<num; di++)
{
radix = (arr[di] / divfac) % 10;
Enqueue(&buckets[radix], arr[di]);
}
for(bi=0, di=0; bi<BUCKET_NUM; bi++)
{
while(!QIsEmpty(&buckets[bi]))
arr[di++] = Dequeue(&buckets[bi]);
}
divfac *= 10;
}
}기수 정렬의 성능
기수 정렬의 성능은 (데이터의 길이) x (데이터의 개수)에 해당하는 이동 연산의 횟수에 따라 결정된다. 따라서, 시간 복잡도는 O(n)인데, 이는 퀵 정렬이나 병합 정렬보다 좋은 성능이다. 물론 사용 가능한 데이터에 제한이 있다는 단점이 있다.
10장 정렬을 모두 공부하고 나니, python의 내장 함수로 있는 sort() 메소드나 sorted() 함수는 어떤 정렬 방식을 쓸지 궁금해졌다. ChatGPT에 물어본 결과, "Timsort" 라고 하는, 본 교재에서 다루지 않은 알고리즘을 쓴다고 하는데, 배운 것 중에서는 병합 정렬과 비슷하다고 한다.

'CS > 자료구조' 카테고리의 다른 글
| [열혈자료구조] 12강. 탐색(Search) 2 : AVL 트리 (1) | 2024.04.27 |
|---|---|
| [열혈자료구조] 11강. 탐색(Search) 1 : 보간탐색, 이진탐색트리 (2) | 2024.04.26 |
| [열혈자료구조] 10강. 정렬(sorting) (1) (1) | 2024.04.16 |
| [열혈자료구조] 9강. 우선순위 큐(Priority Queue)와 힙(heap) (1) | 2024.04.09 |
| [열혈자료구조] 8강. 트리(tree) (1) | 2024.04.08 |