스위칭 대수와 게이트 회로(NAND, NOR, XOR)

* 본 글은 [Introduction to Logic Design, 3rd ed. - Alan B. Marcovitz] 를 바탕으로 작성하였습니다.

 

스위칭 대수는 진리표 혹은 다른 부품으로 구성된 시스템의 해석 및 설계에 필수적이다. "불 대수(boolean algebra)" 로 이루어진 스위칭 대수는, (1) 게이트 회로에서 입력에 대한 출력값을 연산할 때, (2) 아주 복잡한 게이트 회로의 수식을 설계할 때, (3) 게이트 회로를 구현할 때 필수적이다.

 

스위칭 대수란?

스위칭 대수는 모든 변수/상수가 2개의 값(0 혹은 1)으로 된 대수를 말한다. 2진으로 표현되지 않는 변수는 2진으로 코딩된다. 아래는 스위칭 대수의 3가지 연산자이다.

• OR (+): a+b로 나타냄, a=1이거나 b=1일 때, 둘 다 1일 때 1
• AND ( · ): a·b로 나태냄, a=b=1일 때 1
• NOT ( ' ): a'로 나타냄, a=0일 때만 1

AND와 OR gate로 블록도는 아래와 같이 그린다. 참고로, https://app.diagrams.net/ 사이트에서 블록도를 간단히 그릴 수 있다.

 

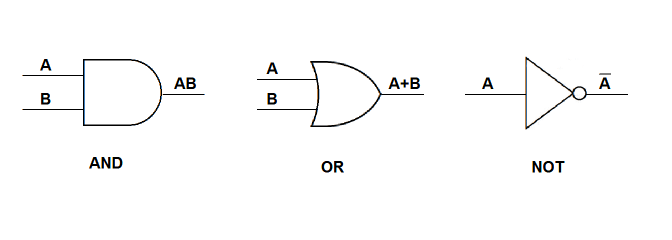
이 연산자들은 아래 성질을 가진다.

 

1) 교환법칙(communicative)

a+b = b+a, ab = ba

 

2) 결합법칙(associative)

a+(b+c) = (a+b)+c, (ab)c = a(bc)

a+b+c+d ... 는 모두 0일 때만 0

abcd...는 모두 1일 때만 1

 

3) 항등원(identity), 널(null), 역원(inverse / complement)

항등원: a+0 = a, a·1 = a

널: a+1 = 1, a·0 = 0

역원: a+a' = 1, aa' = 0

 

4) 멱등(idempotency)

a+a = a, aa = a

 

5) 누승(involution)

(a')' = a

 

6) 분배(distributive)

a(b+c) = ab+ac, a+bc = (a+b)(a+c)

두 번째 식은 한 번에 와 닿지 않을 수 있는데, 진리표를 그려보면 된다.

 

7) 드모르간 정리(DeMorgan's theorem)

(a+b)' = a'b', (ab)' = a' + b'

 

대수 함수의 조작

 

리터럴: 변수 혹은 변수의 보수의 개수, 식의 복잡성을 측정하는 단위

ex) ab' + bc'd + a'd + e'는 8개의 리터럴로 구성됨

 

곱항: 한 개 이상의 리터럴이 AND로 연결된 것, "항"과 비슷한 개념. 주어진 모든 변수에 대한 곱항을 표준곱항 혹은 최소항이라고도 한다.

 

곱의합(SOP, sum of products): 한 개 이상의 곱항들이 OR로 연결된 것.

ex) w'xyz' + wx'y'z' + wx'yz + wxyz는 4 곱항. 특히 이 예시처럼 표준곱항의 합을 정규합이라고 한다.

 

합항: 한 개 이상의 리터럴이 OR로 연결된 것. 마찬가지로 주어진 모든 변수에 대한 합항을 표준합항 혹은 최대항이라고도 한다.

ex) a+b'+c'

 

합의곱(POS, product of sums): 한 개 항의 합항들이 AND로 연결된 것.

ex) (w+x)(w+y)

 

AND, OR, NOT 게이트에 의한 함수 구현

주어진 스위칭 함수를 간단한 식으로 고친 후, 이를 구현하는 회로도를 만든다. 예를 들어, 아래와 같은 스위칭 함수가 있다고 하자.

f = x'yz' + x'yz + xy'z' + xy'z + xyz

 

이는 SOP 형태로 적혀 있으므로, 아래와 같이 회로를 구성하는 것을 생각할 수 있다. 이러한 회로를 2-level 회로라고 하는데, 입력부터 출력까지 통과해야 하는 게이트가 최소 2개이기 때문이다.

 

하지만, 위 함수 f는 아래와 같이 단순화할 수 있다.

f = x'yz' + x'yz + xy'z' + xy'z + xyz  = x'y(z' + z) + xy'(z'+z) + xyz = x'y1 + xy'1 + xyz = x'y + xy' + xyz
 = x'y + x(y' + yz) = x'y + x(y' + z)  =x'y + xy' + xz

 

즉, 아래와 같은 사이즈로 회로를 줄일 수 있는 것이다. 이처럼 최소 곱의합으로 구현하면 회로를 단순화할 수 있다.

 

세 개의 입력 x, y, z를 받아 f를 출력하는 회로를 만든다고 하면, 아래와 같이 입력을 3개로 하여 만들 수도 있다.

 

곱의합이나 합의곱 중 하나로 구현하면, 2-level로 회로를 설계할 수 있으나, 곱의합과 합의곱 모두 아니게 구현하면 회로가 2-level을 초과하게 된다.

 

이러한 게이트는 주로 양쪽 7개씩의 핀을 가지고 있는 DIP(Dual In-line Package) 칩에 들어있고, 집적회로 안에 수 개의 게이트를 가지고 있는 것을 SSI(Small Scale IC)라고 한다. 100개 정도의 게이트를 가지고 있으면 MSI, 그 이상은 LSI, VLSI, GSI... 와 같이 규모가 커진다.

DIP(Dual In-line Package)

 

1960년대에 처음 등장하여 지금도 업계 표준으로 쓰고 있는 DIP 중 7400 시리즈 는 실험실에서 자주 쓰는데, 아래와 같은 기능이 있다.

계열	기능
7404	6(hex) NOT 게이트
7408	4(quad) 2입력 AND 게이트
7411	3(triple) 3입력 AND 게이트
7421	2(dual) 4입력 AND 게이트
7432	4(quad) 2입력 OR 게이트

 

예를 들어 7408을 보면, 아래와 같이 설계된다. 아무것도 연결되지 않은 7번과 14번 핀은 전원 공급용으로 쓴다.

NAND, NOR, XOR 게이트

NAND 게이트

 

NAND 게이트는 AND + NOT이다. 즉, 아래와 같이 구성된다. a, b가 입력되면 (ab)'를 출력하는 것이다.

 

드모르간의 법칙에 따르면 (ab)' = a' + b'이므로, 아래와 같은 형태로 NAND 게이트이다.

 

NAND 게이트의 진리표는 아래와 같다. 두 입력이 모두 1이 들어왔을 때만 0을 출력한다.

a	b	출력
0	0	1
0	1	1
1	0	1
1	1	0

 

실제 회로설계에는 스위칭 대수의 기본 연산인 NOT, AND, OR 대신에 NAND를 더 많이 사용한다. 그 이유는, 이 함수들을 모두 NAND로 대체할 수 있는 완전성(functionally complete)이 있기 때문이다. NAND 회로를 아래와 같이 구성하면 스위칭 대수의 모든 함수를 만들 수 있다.

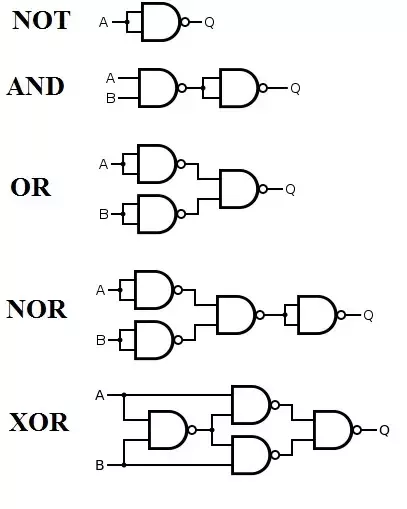
NOR 게이트

 

NOR 게이트는 OR + NOT이다. 즉, 아래와 같이 구성된다. 즉 a, b가 입력되면 (a+b)'를 출력한다.

마찬가지로 드모르간의 법칙에 의해 (a+b)' = a'b'이므로, 아래와 같은 형태도 NOR 게이트이다.

NOR 게이트의 진리표는 아래와 같다. 두 입력이 모두 0이 들어왔을 때만 1을 출력한다.

a	b	출력
0	0	1
0	1	0
1	0	0
1	1	0

 

XOR 게이트

 

XOR 게이트는 Exclusive- OR로, a, b가 입력으로 들어왔을 때 a'b + b'a를 출력한다. 블록도로는 아래와 같이 나타낸다. 위에서 설명했듯, NAND로 XOR 게이트도 구현할 수 있다.

 

XOR 게이트의 진리표는 아래와 같다. 홀수 개의 1이 들어와야 출력이 1이 나온다.

 

a	b	출력
0	0	0
0	1	1
1	0	1
1	1	0