군(group)과 환(ring)

군(group)

이항연산

 

집합 S에 대하여, S의 이항연산(binary operation)이란 S x S에서 S로 mapping 하는 연산을 말한다. 즉, 이항연산 f는 S x S -> S의 map이다. 어떤 이항연산 *에 대하여 *(a, b) = (a*b)로 표기하도록 한다.

 

이항연산은 다음과 같은 두 가지 특징을 가질 수 있다.

1. 결합법칙(associative) : S의 임의의 원소 x, y, z에 대해, (x*y)*z = x*(y*z)
2. 교환법칙(communicative): S의 임의의 원소 x, y에 대해, x*y = y*z

항등원과 역원

 

항등원(identity): 이항연산 *: S x S-> S에 대해, 모든 S의 원소 a에 대하여 a*e = e*a = a인 S의 원소 e가 존재하면 e를 항등원이라고 한다.

 

역원(inverse): 결합법칙이 성립하는 이항연산 *: S x S-> S와, *의 항등원 e에 대해, S의 원소 x의 역원 y는 x*y = y*x = e인 S의 원소로 정의한다.

 

ex) 정수 집합 Z에서, 덧셈에 대한 항등원은 0이고, z의 역원은 -z이다.

 

모노이드, 군, 아벨군

 

 

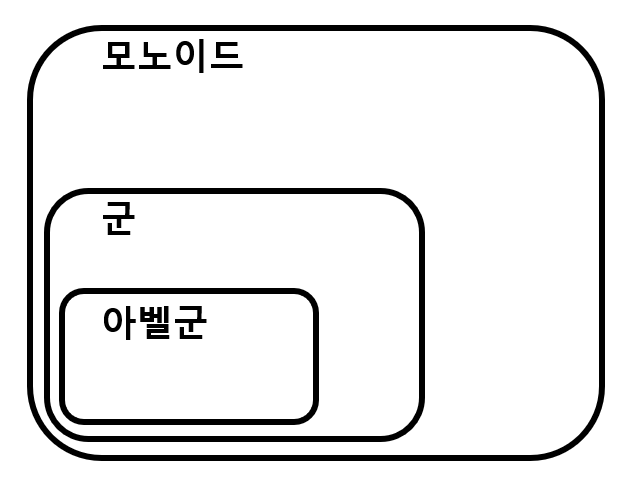
모노이드(monoid): 이항연산 *: S x S-> S에 대해, 다음 두 조건을 만족하는 (S, *)를 모노이드라고 한다.

1. *이 결합법칙을 만족한다.
2. S에 *에 대한 항등원 e가 존재한다.

군(group): 이항연산 *: G x G-> G에 대해, 다음 세 조건을 만족하는 (G, *)를 군이라고 한다.

1. *이 결합법칙을 만족한다.
2. G에 *에 대한 항등원 e가 존재한다.
3. 모든 G의 원소 a에 대한 역원이 존재한다.

아벨군(abelian group / communicative group): 교환법칙이 성립하는 군을 아벨군이라고 한다. 즉, 위 세 조건에 *가 교환법칙이 성립한다는 조건이 추가로 들어간다.

 

ex) 정수집합 Z와 덧셈 +, 곱셈 x에 대해 (Z, +)는 아벨군이다. 반면, (Z, x)에서 결합법칙과 항등원은 있으므로 모노이드이지만, 역원이 존재하지 않는 원소들이 있으므로 군은 아니다.

---

환(Ring)

환(Ring)의 정의: 두 개의 이항연산 #, &이 존재하는 집합 R에 대해, (R, #, &)는 다음 세 조건을 만족할 때 환이다.

1. (R, #)는 아벨군이다.
2. (R, &)는 모노이드이다.
3. R에 속하는 임의의 원소 a, b, c에 대해, a&(b#c) = a&b # a&c이다.

또한, &가 교환법칙을 따를 경우 교환환(communicative ring)이라고 한다.

 

ex) 실수 집합 R과 덧셈 +, 곱셈 x에 대해, (R, +, x)는 교환환이다.

 

이항 관계(binary relation): 집합 X, Y에 대해 이항 관계 R은 X x Y의 원소로 정의된다. 이때 x ~ y for (x, y) in R과 같이 표기한다.

 

동치 관계(equivalence relation): 다음 세 조건을 만족하는 이항 관계를 동치 관계라고 정의한다.

1. reflexibity: a~a가 성립
2. symmetry: a~b iff b~a가 성립
3. transitivity: a~b이고 b~c이면 a~c가 성립

동치류(equivalence class): a와 이항 관계를 가지고 있는 X의 원소 x들의 집합

 

환 동형(ring homomorphism): 항등원 1R, 1S를 가지고 있는 환 R, S에 대해, R에서 S로 가는 환 동형 f: R-> S는 아래 세 조건을 만족한다.

 

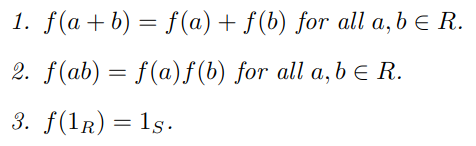
f가 전단사함수일 경우, f를 ring isomorphism이라고 하며, R과 S는 isomorphic이라고 한다.