2025. 1. 18. 03:05ㆍ머신러닝&딥러닝/Explainability
전통적인 XAI 방법론은 특정 input에 대한 feature importance를 분석하는 것이 주된 목표였다. 아래와 같은 saliency map이 대표적인 예시이다. 개를 classify하는 모델을 만들 때, 중요하게 보는 픽셀들을 나타내는 것이다.

하지만 이러한 feature importance는 매우 설명력이 떨어진다. 개라는 사실을 판단하는 데 중요한 것인지, 개가 아니라는 사실을 판단하는 데 중요한 것인지 불확실하며 결국 그 feature들이 어떻게 모델의 판단에 영향을 미치는지를 알 수 없도록 한다.
본 논문에서는 아주 재미있는 방법으로 explainability에 접근하는데, 특정 feature를 점진적으로 강조하거나 소멸시켜서 언제 descision boundary를 넘냐를 보는 것이다. 본문에는 "turning knob"라고 표현이 되어있는데, 문 손잡이처럼 feature가 강조되는 정도를 바꿔 가는 것이다. 이를 Progressive Exaggeration이라고 하며, 이런 방법으로 생성되어 decision boundary를 넘은 데이터 샘플을 Counterfactual Example이라고 한다.
이 논문은 ICLR 2020에 수록되어 주목을 받았으며, 사람이 직관적으로 파악할 수 있는 설명가능성 방법론이기 때문에 각종 데이터에 적용된 사례가 있다.
Introduction
딥러닝이 의료영상 등 고위험 분야에 많이 사용되면서 explainability와 interpretability의 중요성은 점점 높아지고 있다. 이는 data bias를 탐지하고, 모델의 공정성을 평가하는 데 필수적이다.
기존의 설명가능성은 상술한 saliency map이나 removal based method로, 모델이 중요하게 보는 영역을 가렸을 때 판단이 어떻게 달라지는지를 보았다.

하지만 이는 중요한 논리적 비약이 있는데, 우선 원본 이미지를 인위적으로 가린 이미지가 원래 data distribution에 있다고 말하기 힘들다. 즉 실제로 존재할 수 없는 이미지에 대해 평가하는 것이다. 또한, 가렸을 때 모델의 예측이 바뀌지 않았다고 해서 안 중요한 게 아니며, 반대 논리도 마찬가지다.
따라서, 입력 데이터에 점진적으로 변화를 주어 출력 확률을 변화시키며, 언제 decision boundary를 가로지르는지 관찰하는 방법론을 제안하였다. 이는 모델에 무관한(model-agnostic) 방법으로, 특정 모델 구조에 의존하지 않는다.
Method
어떤 모델 (black box)은 입력 공간 X에서 출력 공간 Y로의 매핑 $ f(x) = P(y|x) $로 볼 수 있다. 이때, f의 종류에 상관없이, (1)x에 대한 출력 확률 값과 (2)입력에 대한 gradient $ \nabla_x f(x)$ 에 접근할 수 있다고 가정하자.
이때, 목표는 설명 함수 $I_f (x, \delta)$를 통해 입력 확률에 점진적인 변화를 주어 $f(x)$의 출력을 원하는 확률인 $f(x)+\delta$로 변화시키는 것이다. 설명함수는 입력된 데이터 값과 변화량 $\delta$를 받으며, 아래 세 가지 기준을 만족해야 한다.
- Data Consistency : 생성된 데이터 $x_{\delta}$가 실제와 유사해야 한다.
-> 이는 $\delta$값으로 conditioning된 cGAN을 활용하여 실제와 비슷하게 만든다.
$$ L_\text{cGAN}(D, G) = \mathbb{E}_{x,c}[\log D(x, c)] + \mathbb{E}_{z,c}[\log(1 - D(G(z, c), c))] $$
로 GAN의 loss function을 정의한다. (D : Discriminator, G : Generator) - Black Box Compatibility : $x_{\delta}$를 f에 입력했을 때 원하는 만큼의 확률 변화 ($\delta$)가 발생해야 한다.
-> 이를 위해 loss term에 KL divergence loss를 추가한다.
$$ L_f(D, G) = r(c|x) + D_\text{KL}(f(x) + \delta \| f(x_\delta)) $$ - Self Consistency : $I_f$는 역방향으로 변화 시 원래 상태로 복원되어야 하며, $\delta = 0$일 때 원래 상태로 복원되어야 한다.
-> 이를 위해 loss term에 reconstruction loss와 cycle consistency loss를 추가한다.
Reconstruction : $L_\text{rec}(G) = \|x - G(E(x), c_f(x, 0))\|_1$
Cycle consistency : $ L_\text{cyc}(G) = \|x - G(E(x_\delta), c_f(x, 0))\|_1$
이러한 세 가지를 적용하여, 아래와 같이 괴랄한(?) loss function을 사용하게 된다.
$$ \min_{E, G} \max_{D} \lambda_\text{cGAN} L_\text{cGAN}(D, G) + \lambda_f L_f(D, G) + \lambda_\text{rec} L_\text{rec}(G) + \lambda_\text{rec} L_\text{cyc}(G)$$
그림으로 나타내면 아래와 같이 이해할 수 있다.

Experiments
먼저, loss function에 들어간 세 가지 기준에 대해 평가하는 실험을 진행하였다. 이는 연예인 얼굴 데이터인 CelebA와 X-RAY 데이터셋인 CheXPert로 수행했는데, 아래 그림과 같이 classifier 기준에 따라 feature가 점진적으로 변하는 것을 확인할 수 있다. FID를 이용해 새로 생성된 이미지의 data consistency를 확인하였고, $f(x) + \delta$와 $f(x_{\delta})$의 관계를 평가하여 blackbox compatibility를 평가하였다. 마지막으로 self consistency를 평가하였는데, CelebA에서는 높은 성능을 보였으나 의료 데이터에서는 일부 세부적인 해부학적 구조가 유지되지 않는 경우도 있었다.

특히 이러한 Counterfactual Explanation 기법을 의료 데이터에 적용한 것이 흥미롭다. CheXpert 데이터의 "cardiomegaly" 레이블을 이용하여, 심장 크기의 점진적 변화를 분석하였고, U-Net으로 heart segmentation model을 만들어서 심장 크기를 정량화하였다. 이를 통해, "turning knob"을 돌리는 것과 심장 크기 간 양의 상관관계를 분석하였다.

또한, 양 끝단에 있는 두 이미지의 차이를 이용하여 saliency map을 생성하여 비교하기도 하였다. 이는 다른 gradient 기반의 saliency map보다 우수하다고 한다. 위 그림을 보면, 기존의 propagation 기반 방법론은 미소 부분이 아닌 애매한 지점을 찍는 경우도 있었다.

Data bias가 있는 경우 (성별과 웃음 여부가 correlation이 있는 경우) 모델은 성별 정보와 웃음 정보를 연관짓는다는 것을 확인할 수 있었다.
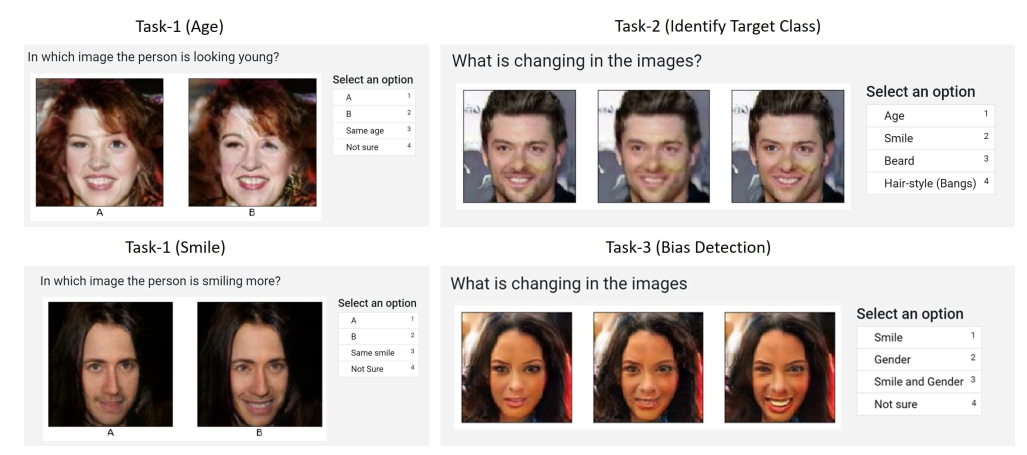
마지막으로, MTurk(Amazon Mechanical Turk) 라는 플랫폼을 사용해서 위와 같이 실제 사용성 설문조사를 진행했다.
'머신러닝&딥러닝 > Explainability' 카테고리의 다른 글
| [XAI] Anthropic의 Mechanistic Interpretability (0) | 2025.01.17 |
|---|---|
| [XAI] Transparent medical image AI via image-text foundation model 논문리뷰 (2) | 2024.12.05 |
| [XAI] HIPPO : ABMIL explainability 논문리뷰 (0) | 2024.12.03 |
| [XAI] LIME : Local Interpretable Model-agnostic Explanation (0) | 2024.12.01 |