GCN의 개요와 수식 정리

GCN은 2016년 Kipf와 Welling의 " Semi-supervised classification with graph convolutional networks" (ICLR 2017)으로 처음 등장하였다. GCN은 일부 노드의 label과 각 노드의 연결관계가 주어진 상태에서 label이 주어지지 않은 노드를 예측하는 node classification을 목적으로 설계되었으나, 전체 그래프에 부여된 label을 예측하는 graph classification에도 사용될 수 있다. Graph classification에서는 일반적인 GCN에 pooling layer가 적용된 형태를 주로 이용한다. 

 

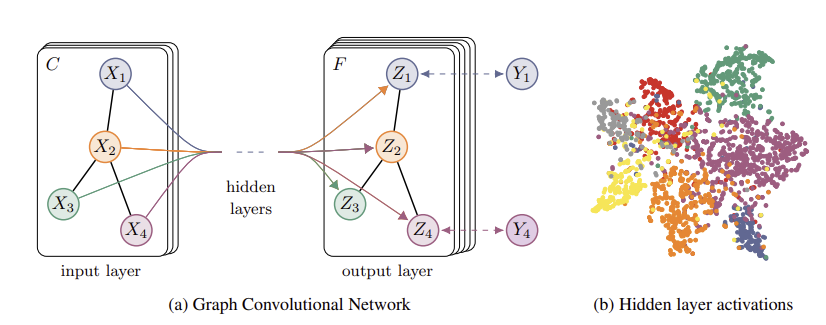
Node classification과 graph classification에서는 Cross Entropy를 적용한 아래 objective function을 사용한다.

 

Node :  $\mathcal{L} = - \sum_{i \in \mathcal{V}_L} \sum_{c=1}^C Y_{ic} \log(\hat{Y}_{ic})
$       ( $ \mathcal{V}_L $ : labeled node 집합)

 

Graph : $\mathcal{L} = - \sum_{j=1}^N \sum_{c=1}^C y_{jc} \log(\hat{y}_{jc})$       ( $j$ : 각 그래프)

 

GCN의 학습과정

GCN의 학습을 위해서는 두 가지 행렬 A와 X가 필요하다. A는 Adjacency matrix로, 어떤 노드가 인접했는지를 나타낸다. X는 Feature matrix로, 각 노드의 feature vector를 저장한다. 즉, N개의 노드에 대해 A는 N x N 크기, X는 N x F의 크기를 가진다.

 

먼저, Adjacency matrix를 이용하여 D라는 행렬(Degree matrix)을 정의한다. Degree matrix는 $D_{ii} = \sum_{j=1}^N A_{ij}$로 정의되며 각 노드가 몇 개의 노드와 연결관계를 가지는지를 나타낸다. 

 

다음으로, 이 D를 이용하여 A를 정규화해 준다. Self-loop (스스로에 대한 연결도 연결이라고 치는 과정)을 포함시켜서, $\tilde{\mathbf{A}} = \mathbf{A} + \mathbf{I}$의 adjacency matrix를 이용할 것이다. 마찬가지로 degree도 $\tilde{\mathbf{D}}_{ii} = \sum_{j=1}^N \tilde{\mathbf{A}}_{ij}$로 다시 정의된다. 이를 $\hat{\mathbf{A}} = \tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-\frac{1}{2}}$로 정규화해주는데, 정규화는 특정 연결이 많은 노드에 계산이 편중되는 것을 막기 위해 한다. (정규화하지 않으면 Degree가 높은 노드는 과도하게 학습되며, degree가 낮은 노드는 상대적으로 간과된다.)

 

이렇게 정규화한 $ \hat{\mathbf{A}} $ 를 feature 및 파라미터 (W) 와 연산하여 활성화 함수에 통과시키는 것이 하나의 layer이다. 즉 하나의 layer의 계산과정은 $\mathbf{H}^{(l+1)} = \sigma\left( \hat{\mathbf{A}} \mathbf{H}^{(l)} \mathbf{W}^{(l)} \right)
$ 이다.

 

GCN은 일반적으로 몇 개 수준의 layer를 적용하는 것이 좋냐에 대해, 2016년 Kipf 논문에서 진행한 실험에 따르면 대충 3개 정도가 적당해 보인다. (물론 데이터의 복잡도에 따라 달라지겠지만)

 

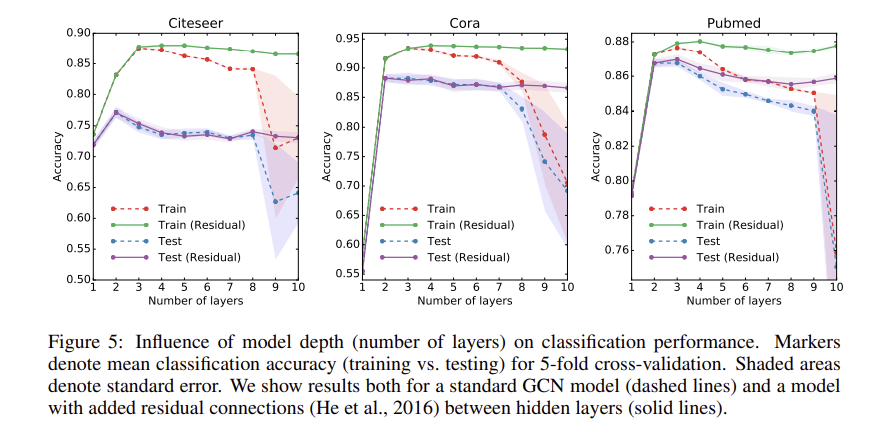
마지막 feature vector의 길이는 클래스 개수 c가 되어 loss function에 바로 태울 수 있게 된다. N = 5짜리 간단한 예시를 들어 보자.

 

예시

친구 a, b, c, d, e 는 취직했거나 백수이다. a, b, c, d는 모두 취직 상태를 알고 있고 e의 취직 상태를 예측한다 해 보자. 다섯 명의 친구관계를 나타낸 adjacency matrix는 아래와 같다.

$$ \mathbf{A} = \begin{bmatrix}
0 & 1 & 1 & 0 & 0 \\
1 & 0 & 0 & 1 & 1 \\
1 & 0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0 & 1 \\
0 & 1 & 1 & 1 & 0
\end{bmatrix} $$

 

여기에 self loop을 추가하자. (단위행렬만 더하면 된다.)

$$\tilde{\mathbf{A}} = \mathbf{A} + \mathbf{I} = \begin{bmatrix}
1 & 1 & 1 & 0 & 0 \\
1 & 1 & 0 & 1 & 1 \\
1 & 0 & 1 & 0 & 1 \\
0 & 1 & 0 & 1 & 1 \\
0 & 1 & 1 & 1 & 1
\end{bmatrix} $$

 

인싸 친구 b와 e는 degree 4를 가지고, 나머지 세 명은 3의 degree를 갖게 된다.

$$\tilde{\mathbf{D}} =\begin{bmatrix}
3 & 0 & 0 & 0 & 0 \\
0 & 4 & 0 & 0 & 0 \\
0 & 0 & 3 & 0 & 0 \\
0 & 0 & 0 & 3 & 0 \\
0 & 0 & 0 & 0 & 4
\end{bmatrix} $$

 

위에서 설명한 수식을 이용하여 A를 정규화하자. (셋째 자리에서 반올림)

$$\hat{\mathbf{A}} = \tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-\frac{1}{2}} = \begin{bmatrix}
0.333 & 0.289 & 0.289 & 0 & 0 \\
0.289 & 0.25 & 0 & 0.289 & 0.289 \\
0.289 & 0 & 0.333 & 0 & 0.289 \\
0 & 0.289 & 0 & 0.333 & 0.289 \\
0 & 0.289 & 0.289 & 0.289 & 0.25
\end{bmatrix} $$

 

취직 유무는 간단히 feature 1개로 나타낼 수 있으므로, 특징행렬은

$$ \mathbf{H}^{(0)} =
\begin{bmatrix}
1 \\
0 \\
1 \\
0 \\
?
\end{bmatrix} $$

 

가 된다.

 

GCN은 행렬 연산이 많이 일어나는데, backprop이 어떻게 일어날까? 여느 신경망과 마찬가지로 $\mathbf{W}^{(l)} \leftarrow \mathbf{W}^{(l)} - \eta \frac{\partial \mathcal{L}}{\partial \mathbf{W}^{(l)}}$이 일어나는데, 여기에 행렬 연산을 적용하면 $\frac{\partial \mathcal{L}}{\partial \mathbf{W}^{(l)}} = \mathbf{H}^{(l)\top} \left( \frac{\partial \mathcal{L}}{\partial \mathbf{H}^{(l+1)}} \circ \sigma'(\mathbf{H}^{(l+1)}) \right) $이 일어난다.

 

응용

1. Node feature masking : 그래프의 node feature중 일부를 마스킹하고 복원하는 task를 통해 self supervised learning을 할 수 있다.

2. Edge prediction : 일부 edge를 제거하고 복원하는 task를 적용

3. Graph Autoencoders : Encoder로 생성한 node feature에 대한 decoder를 활용하여 그래프의 연결관계 A를 복원하는 task 수행